allenai/lila · Datasets at Hugging Face

The chef is having one string of English lower case alphabets only. The chef wants to remove all "abc" special pairs where a,b,c are occurring consecutively. After removing the pair, create a new string and again remove "abc" special pair from a newly formed string. Repeate the process until no such pair remains in a string. -----Input:----- - First line will contain $T$, number of testcases. Then the testcases follow. - Each testcase contains of a single line of input, $String$. -----Output:----- For each testcase, output in a single line answer, new String with no "abc" special pair. -----Constraints:----- $T \leq 2 $ $1 \leq String length \leq 1000 $ -----Sample Input:----- 2 aabcc bababccc -----Sample Output:----- ac bc -----EXPLANATION:----- For 1) after removing "abc" at middle we get a new string as ac. For 2) string = bababccc newString1 = babcc // After removing middle "abc" newString2 = bc //After removing "abc"

t1 = int(input()) for i in range(t1): s1 = input() while("abc" in s1): s1 = s1.replace("abc","") print(s1)

train

APPS_structured

# Task Consider a `bishop`, a `knight` and a `rook` on an `n × m` chessboard. They are said to form a `triangle` if each piece attacks exactly one other piece and is attacked by exactly one piece. Calculate the number of ways to choose positions of the pieces to form a triangle. Note that the bishop attacks pieces sharing the common diagonal with it; the rook attacks in horizontal and vertical directions; and, finally, the knight attacks squares which are two squares horizontally and one square vertically, or two squares vertically and one square horizontally away from its position. ![](https://codefightsuserpics.s3.amazonaws.com/tasks/chessTriangle/img/moves.png?_tm=1473934712872) # Example For `n = 2 and m = 3`, the output should be `8`. 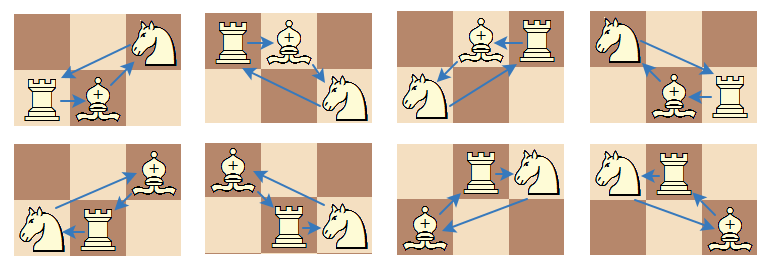![](https://codefightsuserpics.s3.amazonaws.com/tasks/chessTriangle/img/combinations.png?_tm=1473934713038) # Input/Output - `[input]` integer `n` Constraints: `1 ≤ n ≤ 40.` - `[input]` integer `m` Constraints: `1 ≤ m ≤ 40, 3 ≤ n x m`. - `[output]` an integer

clamp = lambda moves, w, h: {(x, y) for x, y in moves if 0 <= x < w and 0 <= y < h} knight = lambda x, y: {(x+u, y+v) for u in range(-2, 3) for v in range(-2, 3) if u*u + v*v == 5} rook = lambda x, y, w, h: {(x, v) for v in range(h)} | {(u, y) for u in range(w)} - {(x, y)} bishop = lambda x, y, w, h: {(x+d*k, y+k) for d in (-1,1) for k in range(-max(x, y), max(w-x, h-y))} - {(x, y)} def search_triangle(x, y, w, h): return sum( len(rook(x, y, w, h) & clamp(bishop(u, v, w, h), w, h)) + len(rook(u, v, w, h) & clamp(bishop(x, y, w, h), w, h)) for u, v in clamp(knight(x, y), w, h) ) def chess_triangle(h, w): wm, hm = min(6, w), min(6, h) return ( sum(search_triangle(min(x, wm-x-1), min(y, hm-y-1), w, h) for x in range(wm) for y in range(hm)) + max(0, w-6) * sum(search_triangle(3, min(y, hm-y-1), w, h) for y in range(hm)) + max(0, h-6) * sum(search_triangle(min(x, wm-x-1), 3, w, h) for x in range(wm)) + max(0, h-6) * max(0, w-6) * search_triangle(3, 3, w, h) )

train

APPS_structured

Given few numbers, you need to print out the digits that are not being used. Example: ```python unused_digits(12, 34, 56, 78) # "09" unused_digits(2015, 8, 26) # "3479" ``` Note: - Result string should be sorted - The test case won't pass Integer with leading zero

def unused_digits(*l): digits_set = set(list("0123456789")) test_set = set("".join(str(i) for i in l)) d = digits_set.difference(test_set) r = "".join(sorted(d)) return r

train

APPS_structured

You are given a set of points in the 2D plane. You start at the point with the least X and greatest Y value, and end at the point with the greatest X and least Y value. The rule for movement is that you can not move to a point with a lesser X value as compared to the X value of the point you are on. Also for points having the same X value, you need to visit the point with the greatest Y value before visiting the next point with the same X value. So, if there are 2 points: (0,4 and 4,0) we would start with (0,4) - i.e. least X takes precedence over greatest Y. You need to visit every point in the plane. -----Input----- You will be given an integer t(1<=t<=20) representing the number of test cases. A new line follows; after which the t test cases are given. Each test case starts with a blank line followed by an integer n(2<=n<=100000), which represents the number of points to follow. This is followed by a new line. Then follow the n points, each being a pair of integers separated by a single space; followed by a new line. The X and Y coordinates of each point will be between 0 and 10000 both inclusive. -----Output----- For each test case, print the total distance traveled by you from start to finish; keeping in mind the rules mentioned above, correct to 2 decimal places. The result for each test case must be on a new line. -----Example----- Input: 3 2 0 0 0 1 3 0 0 1 1 2 2 4 0 0 1 10 1 5 2 2 Output: 1.00 2.83 18.21 For the third test case above, the following is the path you must take: 0,0 -> 1,10 1,10 -> 1,5 1,5 -> 2,2 = 18.21

from math import sqrt def distance_between_two_points(point1,point2): a = (point1[0]-point2[0])**2 + (point1[1]-point2[1])**2 return round(sqrt(a),10) for _ in range(int(input())): blank = input() N = int(input()) dic = {} array = [] for i in range(N): x,y = map(int, input().split()) if x not in dic.keys(): dic[x] = len(array) array.append([x,y,y]) else : index = dic[x] array[index][1] = min(y,array[index][1]) array[index][2] = max(y,array[index][2]) array.sort() ans = 0 length = len(array) for i in range (len(array)-1): ini = array[i] fin = array[i+1] ans+=(ini[2] - ini[1]) ans+=distance_between_two_points([ini[0],ini[1]],[fin[0],fin[2]]) ans += (array[-1][2] - array[-1][1]) print("{:0.2f}".format(ans))

train

APPS_structured

In this Kata, we are going to determine if the count of each of the characters in a string can be equal if we remove a single character from that string. For example: ``` solve('abba') = false -- if we remove any character, the count of each character will not be equal. solve('abbba') = true -- if we remove one b, the count of each character becomes 2. solve('aaaa') = true -- if we remove one character, the remaining characters have same count. solve('wwwf') = true -- if we remove f, the remaining letters have same count. ``` More examples in the test cases. Empty string is not tested. Good luck!

from collections import Counter def solve(s): return any(len(set(Counter(s.replace(c, '', 1)).values())) == 1 for c in s)

train

APPS_structured

In Chefland, types of ingredients are represented by integers and recipes are represented by sequences of ingredients that are used when cooking. One day, Chef found a recipe represented by a sequence $A_1, A_2, \ldots, A_N$ at his front door and he is wondering if this recipe was prepared by him. Chef is a very picky person. He uses one ingredient jar for each type of ingredient and when he stops using a jar, he does not want to use it again later while preparing the same recipe, so ingredients of each type (which is used in his recipe) always appear as a contiguous subsequence. Chef is innovative, too, so he makes sure that in each of his recipes, the quantity of each ingredient (i.e. the number of occurrences of this type of ingredient) is unique ― distinct from the quantities of all other ingredients. Determine whether Chef could have prepared the given recipe. -----Input----- - The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows. - The first line of each test case contains a single integer $N$. - The second line contains $N$ space-separated integers $A_1, A_2, \ldots, A_N$. -----Output----- For each test case, print a single line containing the string "YES" if the recipe could have been prepared by Chef or "NO" otherwise (without quotes). -----Constraints----- - $1 \le T \le 100$ - $1 \le N \le 10^3$ - $1 \le A_i \le 10^3$ for each valid $i$ -----Example Input----- 3 6 1 1 4 2 2 2 8 1 1 4 3 4 7 7 7 8 1 7 7 3 3 4 4 4 -----Example Output----- YES NO NO -----Explanation----- Example case 1: For each ingredient type, its ingredient jar is used only once and the quantities of all ingredients are pairwise distinct. Hence, this recipe could have been prepared by Chef. Example case 2: The jar of ingredient $4$ is used twice in the recipe, so it was not prepared by Chef.

for _ in range(int(input())): N = int(input()) L = list(map(int, input().split())) new = {} for i in L: if i in new.keys(): if i != list(new.keys())[-1]: print('NO') break new[i] += 1 else: new[i] = 0 else: print('YES' if len(new.values()) == len(set(new.values())) else 'NO')

train

APPS_structured

You are given a string $S$. Find the number of ways to choose an unordered pair of non-overlapping non-empty substrings of this string (let's denote them by $s_1$ and $s_2$ in such a way that $s_2$ starts after $s_1$ ends) such that their concatenation $s_1 + s_2$ is a palindrome. Two pairs $(s_1, s_2)$ and $(s_1', s_2')$ are different if $s_1$ is chosen at a different position from $s_1'$ or $s_2$ is chosen at a different position from $s_2'$. -----Input----- The first and only line of the input contains a single string $S$. -----Output----- Print a single line containing one integer — the number of ways to choose a valid pair of substrings. -----Constraints----- - $1 \le |S| \le 1,000$ - $S$ contains only lowercase English letters -----Subtasks----- Subtask #1 (25 points): $|S| \le 100$ Subtask #2 (75 points): original constraints -----Example Input----- abba -----Example Output----- 7 -----Explanation----- The following pairs of substrings can be chosen: ("a", "a"), ("a", "ba"), ("a", "bba"), ("ab", "a"), ("ab", "ba"), ("abb", "a"), ("b", "b").

import sys,math from sys import stdin,stdout s=stdin.readline().strip() ispalin=[[0 for i in range(len(s)+1)] for i in range(len(s)+1)] suff=[[-1 for i in range(len(s)+1)] for i in range(len(s)+1)] pref=[[-1 for i in range(len(s)+1)] for i in range(len(s)+1)] lcp=[[0 for i in range(len(s)+1)] for i in range(len(s)+1)] for i in range(0,len(s)): ispalin[i][i]=1;pref[i][i]=1;suff[i][i]=1 ispalin[i][i+1]=1;pref[i][i+1]=2;suff[i][i+1]=2 #for i in ispalin: #print(i) for l in range(2,len(s)+1): for i in range(0,len(s)-l+1): #print(i,i+l-1,s[i],s[i+l-1]) ispalin[i][i+l]=ispalin[i+1][i+l-1]*int(s[i]==s[i+l-1]) pref[i][i+l]=pref[i][i+l-1]+ispalin[i][i+l] suff[i][i+l]=suff[i+1][i+l]+ispalin[i][i+l] for i in range(len(s)): for j in range(i+1,len(s)): lcp[i][j]=(lcp[i-1][j+1]+1)*int(s[i]==s[j]) # ans=0 for i in range(1,len(s)): for j in range(i,len(s)): #if lcp[i-1][j]!=0: #print(i,j,lcp[i-1][j],suff[i][j],pref[i][j],s[0:i],s[i:j],s[j:]) ans+=(lcp[i-1][j]*(suff[i][j]+pref[i][j]-1)) # stdout.write(str(ans))

train

APPS_structured

Write a class Random that does the following: 1. Accepts a seed ```python >>> random = Random(10) >>> random.seed 10 ``` 2. Gives a random number between 0 and 1 ```python >>> random.random() 0.347957 >>> random.random() 0.932959 ``` 3. Gives a random int from a range ```python >>> random.randint(0, 100) 67 >>> random.randint(0, 100) 93 ``` Modules `random` and `os` are forbidden. Dont forget to give feedback and your opinion on this kata even if you didn't solve it!

class Random(): def __init__(self, seed): self.seed = seed def random(self): self.seed = (4123*self.seed+4321)%4096 #whatever return self.seed/4096 def randint(self, start, end): return int(start + (end-start)*self.random())

train

APPS_structured

Your task is to determine the top 3 place finishes in a pole vault competition involving several different competitors. This is isn't always so simple, and it is often a source of confusion for people who don't know the actual rules. Here's what you need to know: As input, you will receive an array of objects. Each object contains the respective competitor's name (as a string) and his/her results at the various bar heights (as an array of strings): [{name: "Sergey", results: ["", "O", "XO", "O", "XXO", "XXX", "", ""]}{name: "Jan", results: ["", "", "", "O", "O", "XO", "XXO", "XXX"]}{name: "Bruce", results: ["", "XO", "XXO", "XXX", "", "", "", ""]}{name: "HerrWert", results: ["XXX", "", "", "", "", "", "", ""]}] In the array of strings described above, each string represents the vaulter's performance at a given height. The possible values are based on commonly used written notations on a pole vault scoresheet: An empty string indicates that the vaulter did not jump at this height for a variety of possible reasons ("passed" at this height, was temporarily called away to a different track and field event, was already eliminated from competition, or withdrew due to injury, for example).An upper-case X in the string represents an unsuccessful attempt at the height. (As you may know, the vaulter is eliminated from the competition after three consecutive failed attempts.)An upper-case O represents a successful attempt. If present at all, this will be the final character in the string, because it indicates that the vaulter has now successfully completed this height and is ready to move on. All vaulters will have a result string (though possibly empty) for every height involved in the competition, making it possible to match up the results of different vaulters with less confusion. Obviously, your first task is to determine who cleared the greatest height successfully. In other words, who has a "O" mark at a higher array element than any other competitor? You might want to work through the arrays from right to left to determine this. In the most straightforward case, you would first determine the winner, then second place, and finally third place by this simple logic. But what if there's a tie for one of these finishing places? Proceed as follows (according to American high school rules, at least): First trace backwards to find the greatest height that both vaulters cleared successfully. Then determine who had the fewest unsuccessful attempts at this height (i.e., the fewest X's in the string for this height). This person wins the tie-break.But what if they're still tied with one another? Do NOT continue to trace backwards through the heights! Instead, compare their total numbers of unsuccessful attempts at all heights in the competition. The vaulter with the fewest total misses wins the tie-break.But what if they're still tied? It depends on the finishing place:If it's for second or third place, the tie stands (i.e., is not broken).But if it's for first place, there must be a jump-off (like overtime or penalty kicks in other sports) to break the tie and determine the winner. (This jump-off occurs - hypothetically - after your code runs and is thus not a part of this kata.) Return a single object as your result. Each place-finish that is included in the results (including at least first place as property "1st" and possibly second and third places as properties "2nd" and "3rd") should have as its value the respective vaulter's name. In the event of a tie, the value of the property is the names of all tied vaulters, in alphabetical order, separated by commas, and followed by the notation "(jump-off)" if the tie is for first place or "(tie)" if it's for second or third place. Here are some possible outcomes to show you what I mean: {1st: "Jan", 2nd: "Sergey"; 3rd: "Bruce"} (These results correspond to the sample input data given above.){1st: "Julia", 2nd: "Madi, Emily (tie)}"{1st: "Caleb, Dustin (jump-off)", 3rd: "Sam"}{1st: "Meredith", 2nd: "Maddy", 3rd: "Cierra, Sara (tie)"}{1st: "Alex, Basti, Max (jump-off)"} If you are familiar with the awarding of place finishes in sporting events or team standings in a league, then you know that there won't necessarily be a 2nd or 3rd place, because ties in higher places "bump" all lower places downward accordingly. One more thing: You really shouldn't change the array of objects that you receive as input. This represents the physical scoresheet. We need this "original document" to be intact, so that we can refer back to it to resolve a disputed result! Have fun with this! - - - - - Notes for the Python version: The rules for the Python version are the same as the original JavaScript version. The input and output will look the same as the JavaScript version. But, the JavaScript objects will be replaced by Python dictionaries. The JavaScript arrays will be replaced by Python lists. The Python function name was changed to include underscores as is customary with Python names. The example below should help clarify all of this. The input for the Python version will be a list containing dictionaries with the competitors' names and results. The names in the dictionaries are strings. The results are lists with a list of strings. And example follows. score_pole_vault([ {"name": "Linda", "results": ["XXO", "O","XXO", "O"]}, {"name": "Vickie", "results": ["O","X", "", ""]}, {"name": "Debbie", "results": ["XXO", "O","XO", "XXX"]}, {"name": "Michelle", "results": ["XO","XO","XXX",""]}, {"name": "Carol", "results": ["XXX", "","",""]} ]) The returned results should be in a dictionary with one to three elements. Examples of possible returned results: {'1st': 'Linda', '2nd': 'Debbie', '3rd': 'Michelle'} {'1st': 'Green, Hayes (jump-off)', '3rd': 'Garcia'} Note: Since first place was tied in this case, there is no 2nd place awarded. {'1st': 'Wilson', '2nd': 'Laurie', '3rd': 'Joyce, Moore (tie)'} I have tried to create test cases that have every concievable tie situation. Have fun with this version, as well!

def score_pole_vault(vaulter_list): summary=[] for i in vaulter_list: total_X=0 highest_cleared=-1 X_at_highest = 0 for j in range(len(i["results"])): if "O" in i["results"][j]: highest_cleared=j X_at_highest=i["results"][j].count("X") total_X += i["results"][j].count("X") summary.append((-highest_cleared, X_at_highest, total_X, i["name"])) final_standing= sorted(summary) result = {} winners_stat= final_standing[0][:3] winners=[] for i in final_standing: if i[:3]==winners_stat[:3]: winners.append(i[3]) result["1st"] = ", ".join(winners) + " (jump-off)"*(len(winners)>1) if len(winners)>2: return result if len(winners)==1: second_stat= final_standing[1][:3] seconds=[] for i in final_standing: if i[:3]==second_stat[:3]: seconds.append(i[3]) result["2nd"] = ", ".join(seconds) + " (tie)"*(len(seconds)>1) if len(seconds)>1: return result thirds=[] third_stat = final_standing[2][:3] for i in final_standing: if i[:3]==third_stat[:3]: thirds.append(i[3]) result["3rd"] = ", ".join(thirds) + " (tie)"*(len(thirds)>1) return result

train

APPS_structured

The Little Elephant has an integer a, written in the binary notation. He wants to write this number on a piece of paper. To make sure that the number a fits on the piece of paper, the Little Elephant ought to delete exactly one any digit from number a in the binary record. At that a new number appears. It consists of the remaining binary digits, written in the corresponding order (possible, with leading zeroes). The Little Elephant wants the number he is going to write on the paper to be as large as possible. Help him find the maximum number that he can obtain after deleting exactly one binary digit and print it in the binary notation. -----Input----- The single line contains integer a, written in the binary notation without leading zeroes. This number contains more than 1 and at most 10^5 digits. -----Output----- In the single line print the number that is written without leading zeroes in the binary notation — the answer to the problem. -----Examples----- Input 101 Output 11 Input 110010 Output 11010 -----Note----- In the first sample the best strategy is to delete the second digit. That results in number 11_2 = 3_10. In the second sample the best strategy is to delete the third or fourth digits — that results in number 11010_2 = 26_10.

sa=input() lo=[] if '0' in sa: for char in sa: lo.append(char) for element in lo: if element=='0': lo.remove(element) break string='' for element in lo: string+=element print(string) else: print(sa[1:])

train

APPS_structured

Given a string, you progressively need to concatenate the first letter from the left and the first letter to the right and "1", then the second letter from the left and the second letter to the right and "2", and so on. If the string's length is odd drop the central element. For example: ```python char_concat("abcdef") == 'af1be2cd3' char_concat("abc!def") == 'af1be2cd3' # same result ```

def char_concat(w): n = len(w)//2 return "".join(c[0]+c[1]+str(i+1) for i, c in enumerate(zip(w[:n], w[:-n-1:-1])))

train

APPS_structured

You are given two integers N$N$ and M$M$. You have to construct a matrix with N$N$ rows and M$M$ columns. Consider a multiset S$S$ which contains N+M$N + M$ integers: for each row and each column of this matrix, the MEX of the elements of this row/column belongs to S$S$. Then, in the matrix you construct, the MEX of S$S$ must be maximum possible. Note: The MEX of a multiset of integers is the smallest non-negative integer that is not present in this multiset. For example, MEX({4,9,0,1,1,5})=2$\mathrm{MEX}(\{4,9,0,1,1,5\}) = 2$ and MEX({1,2,3})=0$\mathrm{MEX}(\{1,2,3\}) = 0$. -----Input----- - The first line of the input contains a single integer T$T$ denoting the number of test cases. The description of T$T$ test cases follows. - The first and only line of each test case contains two space-separated integers N$N$ and M$M$. -----Output----- For each test case, print N$N$ lines. For each i$i$ (1≤i≤N$1 \le i \le N$), the i$i$-th of these lines should contain M$M$ space-separated integers ― the elements in the i$i$-th row of your matrix. Each element of the matrix must be non-negative and must not exceed 109$10^9$. If there are multiple solutions, you may find any one of them. -----Constraints----- - 1≤T≤400$1 \le T \le 400$ - 1≤N,M≤100$1 \le N, M \le 100$ - the sum of N⋅M$N \cdot M$ over all test cases does not exceed 105$10^5$ -----Example Input----- 2 3 3 4 2 -----Example Output----- 9 1 0 1 0 2 7 5 8 2 2 3 0 1 1 0 1 -----Explanation----- Example case 1: The MEXs of the rows {9,1,0}$\{9, 1, 0\}$, {1,0,2}$\{1, 0, 2\}$ and {7,5,8}$\{7, 5, 8\}$ are 2$2$, 3$3$ and 0$0$ respectively. The MEXs of the columns {9,1,7}$\{9, 1, 7\}$, {1,0,5}$\{1, 0, 5\}$ and {0,2,8}$\{0, 2, 8\}$ are 0$0$, 2$2$ and 1$1$ respectively. Therefore, the multiset which contains the MEX of each row and each column is S={0,0,1,2,2,3}$S = \{0, 0, 1, 2, 2, 3\}$ and MEX(S)=4$\mathrm{MEX}(S) = 4$. We can show that this is the largest MEX that can be obtained for a 3×3$3 \times 3$ matrix.

# import all important libraries and inbuilt functions from fractions import Fraction import numpy as np import sys,bisect,copyreg,statistics,os,time,socket,socketserver,atexit from math import gcd,ceil,floor,sqrt,copysign,factorial,fmod,fsum from math import expm1,exp,log,log2,acos,asin,cos,tan,sin,pi,e,tau,inf,nan from collections import Counter,defaultdict,deque,OrderedDict from itertools import combinations,permutations,accumulate,groupby from numpy.linalg import matrix_power as mp from bisect import bisect_left,bisect_right,bisect,insort,insort_left,insort_right from statistics import mode from copy import copy from functools import reduce,cmp_to_key from io import BytesIO, IOBase from scipy.spatial import ConvexHull from heapq import * from decimal import * from queue import Queue,PriorityQueue from re import sub,subn from random import shuffle,randrange,randint,random # never import pow from math library it does not perform modulo # use standard pow -- better than math.pow # end of library import # map system version faults if sys.version_info[0] < 3: from builtins import xrange as range from future_builtins import ascii, filter, hex, map, oct, zip # template of many functions used in competitive programming can add more later # based on need we will use this commonly. # bfs in a graph def bfs(adj,v): # a schema of bfs visited=[False]*(v+1);q=deque() while q:pass # definition of vertex of a graph def graph(vertex): return [[] for i in range(vertex+1)] def lcm(a,b): return (a*b)//gcd(a,b) # most common list in a array of lists def most_frequent(List):return Counter(List).most_common(1)[0][0] # element with highest frequency def most_common(List):return(mode(List)) #In number theory, the Chinese remainder theorem states that #if one knows the remainders of the Euclidean division of an integer n by #several integers, then one can determine uniquely the remainder of the #division of n by the product of these integers, under the condition #that the divisors are pairwise coprime. def chinese_remainder(a, p): prod = reduce(op.mul, p, 1);x = [prod // pi for pi in p] return sum(a[i] * pow(x[i], p[i] - 2, p[i]) * x[i] for i in range(len(a))) % prod # make a matrix def createMatrix(rowCount, colCount, dataList): mat = [] for i in range (rowCount): rowList = [] for j in range (colCount): if dataList[j] not in mat:rowList.append(dataList[j]) mat.append(rowList) return mat # input for a binary tree def readTree(): v=int(inp());adj=[set() for i in range(v+1)] for i in range(v-1):u1,u2=In(); adj[u1].add(u2);adj[u2].add(u1) return adj,v # sieve of prime numbers def sieve(): li=[True]*1000001;li[0],li[1]=False,False;prime=[] for i in range(2,len(li),1): if li[i]==True: for j in range(i*i,len(li),i):li[j]=False for i in range(1000001): if li[i]==True:prime.append(i) return prime #count setbits of a number. def setBit(n): count=0 while n!=0:n=n&(n-1);count+=1 return count # sum of digits of a number def digitsSum(n): if n == 0:return 0 r = 0 while n > 0:r += n % 10;n //= 10 return r # ncr efficiently def ncr(n, r): r = min(r, n - r);numer = reduce(op.mul, list(range(n, n - r, -1)), 1);denom = reduce(op.mul, list(range(1, r + 1)), 1) return numer // denom # or / in Python 2 #factors of a number def factors(n):return list(set(reduce(list.__add__, ([i, n // i] for i in range(1, int(n**0.5) + 1) if n % i == 0)))) #prime fators of a number def prime_factors(n): i = 2;factors = [] while i * i <= n: if n % i:i += 1 else:n //= i;factors.append(i) if n > 1:factors.append(n) return set(factors) def prefixSum(arr): for i in range(1, len(arr)):arr[i] = arr[i] + arr[i-1] return arr def binomial_coefficient(n, k): if 0 <= k <= n: ntok = 1;ktok = 1 for t in range(1, min(k, n - k) + 1):ntok *= n;ktok *= t;n -= 1 return ntok // ktok else:return 0 def powerOfK(k, max): if k == 1:return [1] if k == -1:return [-1, 1] result = [];n = 1 while n <= max:result.append(n);n *= k return result # maximum subarray sum use kadane's algorithm def kadane(a,size): max_so_far = 0;max_ending_here = 0 for i in range(0, size): max_ending_here = max_ending_here + a[i] if (max_so_far < max_ending_here):max_so_far = max_ending_here if max_ending_here < 0:max_ending_here = 0 return max_so_far def divisors(n): result = [] for i in range(1,ceil(sqrt(n))+1): if n%i == 0: if n/i == i:result.append(i) else:result.append(i);result.append(n/i) return result def sumtilln(n): return ((n*(n+1))//2) def isPrime(n) : if (n <= 1) :return False if (n <= 3) :return True if (n % 2 == 0 or n % 3 == 0) :return False for i in range(5,ceil(sqrt(n))+1,6): if (n % i == 0 or n % (i + 2) == 0) :return False return True def isPowerOf2(n): while n % 2 == 0:n //= 2 return (True if n == 1 else False) def power2(n): k = 0 while n % 2 == 0:k += 1;n //= 2 return k def sqsum(n):return ((n*(n+1))*(2*n+1)//6) def cusum(n):return ((sumn(n))**2) def pa(a): for i in range(len(a)):print(a[i], end = " ") print() def pm(a,rown,coln): for i in range(rown): for j in range(coln):print(a[i][j],end = " ") print() def pmasstring(a,rown,coln): for i in range(rown): for j in range(coln):print(a[i][j],end = "") print() def isPerfectSquare(n):return pow(floor(sqrt(n)),2) == n def nC2(n,m):return (((n*(n-1))//2) % m) def modInverse(n,p):return pow(n,p-2,p) def ncrmodp(n, r, p): num = den = 1 for i in range(r):num = (num * (n - i)) % p ;den = (den * (i + 1)) % p return (num * pow(den,p - 2, p)) % p def reverse(string):return "".join(reversed(string)) def listtostr(s):return ' '.join([str(elem) for elem in s]) def binarySearch(arr, l, r, x): while l <= r: mid = l + (r - l) // 2; if arr[mid] == x:return mid elif arr[mid] < x:l = mid + 1 else:r = mid - 1 return -1 def isarrayodd(a): r = True for i in range(len(a)): if a[i] % 2 == 0: r = False break return r def isarrayeven(a): r = True for i in range(len(a)): if a[i] % 2 == 1: r = False break return r def isPalindrome(s):return s == s[::-1] def gt(x,h,c,t):return ((x*h+(x-1)*c)/(2*x-1)) def CountFrequency(my_list): freq = {} for item in my_list:freq[item] = (freq[item] + 1 if (item in freq) else 1) return freq def CountFrequencyasPair(my_list1,my_list2,freq): for item in my_list1:freq[item][0] = (freq[item][0] + 1 if (item in freq) else 1) for item in my_list2:freq[item][1] = (freq[item][1] + 1 if (item in freq) else 1) return freq def binarySearchCount(arr, n, key): left = 0;right = n - 1;count = 0 while (left <= right): mid = int((right + left) / 2) if (arr[mid] <= key):count,left = mid + 1,mid + 1 else:right = mid - 1 return count def primes(n): sieve,l = [True] * (n+1),[] for p in range(2, n+1): if (sieve[p]): l.append(p) for i in range(p, n+1, p):sieve[i] = False return l def Next_Greater_Element_for_all_in_array(arr): s,n,reta,retb = list(),len(arr),[],[];arr1 = [list([0,i]) for i in range(n)] for i in range(n - 1, -1, -1): while (len(s) > 0 and s[-1][0] <= arr[i]):s.pop() if (len(s) == 0):arr1[i][0] = -1 else:arr1[i][0] = s[-1] s.append(list([arr[i],i])) for i in range(n):reta.append(list([arr[i],i]));retb.append(arr1[i][0]) return reta,retb def polygonArea(X,Y,n): area = 0.0;j = n - 1 for i in range(n):area += (X[j] + X[i]) * (Y[j] - Y[i]);j = i return abs(area / 2.0) def merge(a, b): ans = defaultdict(int) for i in a:ans[i] += a[i] for i in b:ans[i] += b[i] return ans def subarrayBitwiseOR(A): res,pre = set(),{0} for x in A: pre = {x | y for y in pre} | {x} ;res |= pre return len(res) # Print the all possible subset sums that lie in a particular interval of l <= sum <= target def subset_sum(numbers,l,target, partial=[]): s = sum(partial) if l <= s <= target:print("sum(%s)=%s" % (partial, s)) if s >= target:return for i in range(len(numbers)):subset_sum(numbers[i+1:], l,target, partial + [numbers[i]]) #defining a LRU Cache # where we can set values and get values based on our requirement class LRUCache: # initialising capacity def __init__(self, capacity: int): self.cache = OrderedDict() self.capacity = capacity # we return the value of the key # that is queried in O(1) and return -1 if we # don't find the key in out dict / cache. # And also move the key to the end # to show that it was recently used. def get(self, key: int) -> int: if key not in self.cache:return -1 else:self.cache.move_to_end(key);return self.cache[key] # first, we add / update the key by conventional methods. # And also move the key to the end to show that it was recently used. # But here we will also check whether the length of our # ordered dictionary has exceeded our capacity, # If so we remove the first key (least recently used) def put(self, key: int, value: int) -> None: self.cache[key] = value;self.cache.move_to_end(key) if len(self.cache) > self.capacity:self.cache.popitem(last = False) class segtree: def __init__(self,n): self.m = 1 while self.m < n:self.m *= 2 self.data = [0] * (2 * self.m) def __setitem__(self,i,x): x = +(x != 1);i += self.m;self.data[i] = x;i >>= 1 while i:self.data[i] = self.data[2 * i] + self.data[2 * i + 1];i >>= 1 def __call__(self,l,r): l += self.m;r += self.m;s = 0 while l < r: if l & 1:s += self.data[l];l += 1 if r & 1:r -= 1;s += self.data[r] l >>= 1;r >>= 1 return s class FenwickTree: def __init__(self, n):self.n = n;self.bit = [0]*(n+1) def update(self, x, d): while x <= self.n:self.bit[x] += d;x += (x & (-x)) def query(self, x): res = 0 while x > 0:res += self.bit[x];x -= (x & (-x)) return res def range_query(self, l, r):return self.query(r) - self.query(l-1) # can add more template functions here # end of template functions # To enable the file I/O i the below 2 lines are uncommented. # read from in.txt if uncommented if os.path.exists('in.txt'): sys.stdin=open('in.txt','r') # will print on Console if file I/O is not activated #if os.path.exists('out.txt'): sys.stdout=open('out.txt', 'w') # inputs template #for fast input we areusing sys.stdin def inp(): return sys.stdin.readline().strip() #for fast output, always take string def out(var): sys.stdout.write(str(var)) # custom base input needed for the program def I():return (inp()) def II():return (int(inp())) def FI():return (float(inp())) def SI():return (list(str(inp()))) def MI():return (map(int,inp().split())) def LI():return (list(MI())) def SLI():return (sorted(LI())) def MF():return (map(float,inp().split())) def LF():return (list(MF())) def SLF():return (sorted(LF())) # end of inputs template # common modulo values used in competitive programming MOD = 998244353 mod = 10**9+7 # any particular user-defined functions for the code. # can be written here. # Python implementation of the above approach # function to return count of distinct bitwise OR # end of any user-defined functions # main functions for execution of the program. def __starting_point(): # execute your program from here. # start your main code from here # Write your code here for _ in range(II()): n,m = MI() x,y,a = max(n,m),min(n,m),0 dp = [[0 for _ in range(y)] for i in range(x)] if m == n : for i in range(x): a = i for j in range(y): dp[i][j] = a % (y + 1) a += 1 dp[-1][0] = y else: for i in range(y+1): for j in range(y): dp[i][j] = a % (y+1) a += 1 a,t = y + 1,0 for i in range(y+1,x): for j in range(y):dp[i][j] = a a += 1 try : dp[i][t] = a except: pass t += 1 if x == n and y == m: for i in dp:print(*i) else: z = [] for i in range(y): z.append([]) for j in range(x): z[i].append(dp[j][i]) for i in z:print(*i) # end of main code # end of program # This program is written by : # Shubham Gupta # B.Tech (2019-2023) # Computer Science and Engineering, # Department of EECS # Contact No:8431624358 # Indian Institute of Technology(IIT),Bhilai # Sejbahar, # Datrenga, # Raipur, # Chhattisgarh # 492015 # THANK YOU FOR #YOUR KIND PATIENCE FOR READING THE PROGRAM. __starting_point()

train

APPS_structured

It's autumn now, the time of the leaf fall. Sergey likes to collect fallen leaves in autumn. In his city, he can find fallen leaves of maple, oak and poplar. These leaves can be of three different colors: green, yellow or red. Sergey has collected some leaves of each type and color. Now he wants to create the biggest nice bouquet from them. He considers the bouquet nice iff all the leaves in it are either from the same type of tree or of the same color (or both). Moreover, he doesn't want to create a bouquet with even number of leaves in it, since this kind of bouquets are considered to attract bad luck. However, if it's impossible to make any nice bouquet, he won't do anything, thus, obtaining a bouquet with zero leaves. Please help Sergey to find the maximal number of leaves he can have in a nice bouquet, which satisfies all the above mentioned requirements. Please note that Sergey doesn't have to use all the leaves of the same color or of the same type. For example, if he has 20 maple leaves, he can still create a bouquet of 19 leaves. -----Input----- IThe first line of the input contains an integer T denoting the number of test cases. The description of T test cases follows." The first line of each test case contains three space-separated integers MG MY MR denoting the number of green, yellow and red maple leaves respectively. The second line contains three space-separated integers OG OY OR denoting the number of green, yellow and red oak leaves respectively. The third line of each test case contains three space-separated integers PG PY PR denoting the number of green, yellow and red poplar leaves respectively. -----Output----- For each test case, output a single line containing the maximal amount of flowers in nice bouquet, satisfying all conditions or 0 if it's impossible to create any bouquet, satisfying the conditions. -----Constraints----- - 1 ≤ T ≤ 10000 - Subtask 1 (50 points): 0 ≤ MG, MY, MR, OG, OY, OR, PG, PY, PR ≤ 5 - Subtask 2 (50 points): 0 ≤ MG, MY, MR, OG, OY, OR, PG, PY, PR ≤ 109 -----Example----- Input:1 1 2 3 3 2 1 1 3 4 Output:7 -----Explanation----- Example case 1. We can create a bouquet with 7 leaves, for example, by collecting all yellow leaves. This is not the only way to create the nice bouquet with 7 leaves (for example, Sergey can use all but one red leaves), but it is impossible to create a nice bouquet with more than 7 leaves.

for t in range(int(input())): l1=list(map(int,input().split())) l2=list(map(int,input().split())) l3=list(map(int,input().split())) max=0 g=l1[0]+l2[0]+l3[0] y=l1[1]+l2[1]+l3[1] r=l1[2]+l2[2]+l3[2] if g%2==0: g-=1 if y%2==0: y-=1 if r%2==0: r-=1 if max<g: max=g if max<r: max=r if max<y: max=y m=l1[0]+l1[1]+l1[2] o=l2[0]+l2[1]+l2[2] p=l3[0]+l3[1]+l3[2] if m%2==0: m-=1 if o%2==0: o-=1 if p%2==0: p-=1 if max<m: max=m if max<o: max=o if max<p: max=p print(max)

train

APPS_structured

This time minions are celebrating Diwali Festival. There are N minions in total. Each of them owns a house. On this Festival, Each of them wants to decorate their house. But none of them have enough money to do that. One of the minion, Kevin, requested Gru for money. Gru agreed for money distribution but he will be giving money to a minion if and only if demanded money is less than or equal to the money Gru have. Now Gru wonders if he can spend all the money or not. -----Input----- First line have number of test cases T. Each test case consist of Two Lines. First line contains two space separated integers N and K i.e. Number of minions and Amount of Money Gru have. Next line contains N space separated integers A1,A2,A3,.....,AN representing amount of money demanded by ith minion. -----Output----- Output YES if Gru can spend his all of the money on minions i.e. after distribution Gru have zero amount of money else NO. -----Constraints----- - 1 ≤ T ≤ 105 - 1 ≤ N ≤ 102 - 1 ≤ K,Ai ≤ 109 -----Example----- Input: 2 4 9 5 2 2 4 4 9 5 2 18 3 Output: YES NO -----Explanation----- Example case 1.At first Gru is having 9 Rs. If he gives 5 Rs. to first minion then remaining 4 Rs. can be given to 2nd and 3rd minion or to the 4th minion. Which will leave zero amount of money in the hands of Gru. Example case 2.At first Gru is having 9 Rs. If he gives 5 Rs. to the first minion then from remaining 4 Rs. either he can give 2 Rs. to the 2nd minion or 3 Rs. to the fourth minion. Which will leave either 2 Rs. or 1 Rs. in the hands of Gru.

def find_combinations(list, sum): if not list: if sum == 0: return [[]] return [] return find_combinations(list[1:], sum) + \ [[list[0]] + tail for tail in find_combinations(list[1:], sum - list[0])] for tc in range(int(input())): n,k=list(map(int,input().split())) a=list(map(int,input().split())) a.sort() if len(find_combinations(a,k))==0: print("NO") else: print("YES")

train

APPS_structured

There are $n$ lamps on a line, numbered from $1$ to $n$. Each one has an initial state off ($0$) or on ($1$). You're given $k$ subsets $A_1, \ldots, A_k$ of $\{1, 2, \dots, n\}$, such that the intersection of any three subsets is empty. In other words, for all $1 \le i_1 < i_2 < i_3 \le k$, $A_{i_1} \cap A_{i_2} \cap A_{i_3} = \varnothing$. In one operation, you can choose one of these $k$ subsets and switch the state of all lamps in it. It is guaranteed that, with the given subsets, it's possible to make all lamps be simultaneously on using this type of operation. Let $m_i$ be the minimum number of operations you have to do in order to make the $i$ first lamps be simultaneously on. Note that there is no condition upon the state of other lamps (between $i+1$ and $n$), they can be either off or on. You have to compute $m_i$ for all $1 \le i \le n$. -----Input----- The first line contains two integers $n$ and $k$ ($1 \le n, k \le 3 \cdot 10^5$). The second line contains a binary string of length $n$, representing the initial state of each lamp (the lamp $i$ is off if $s_i = 0$, on if $s_i = 1$). The description of each one of the $k$ subsets follows, in the following format: The first line of the description contains a single integer $c$ ($1 \le c \le n$) — the number of elements in the subset. The second line of the description contains $c$ distinct integers $x_1, \ldots, x_c$ ($1 \le x_i \le n$) — the elements of the subset. It is guaranteed that: The intersection of any three subsets is empty; It's possible to make all lamps be simultaneously on using some operations. -----Output----- You must output $n$ lines. The $i$-th line should contain a single integer $m_i$ — the minimum number of operations required to make the lamps $1$ to $i$ be simultaneously on. -----Examples----- Input 7 3 0011100 3 1 4 6 3 3 4 7 2 2 3 Output 1 2 3 3 3 3 3 Input 8 6 00110011 3 1 3 8 5 1 2 5 6 7 2 6 8 2 3 5 2 4 7 1 2 Output 1 1 1 1 1 1 4 4 Input 5 3 00011 3 1 2 3 1 4 3 3 4 5 Output 1 1 1 1 1 Input 19 5 1001001001100000110 2 2 3 2 5 6 2 8 9 5 12 13 14 15 16 1 19 Output 0 1 1 1 2 2 2 3 3 3 3 4 4 4 4 4 4 4 5 -----Note----- In the first example: For $i = 1$, we can just apply one operation on $A_1$, the final states will be $1010110$; For $i = 2$, we can apply operations on $A_1$ and $A_3$, the final states will be $1100110$; For $i \ge 3$, we can apply operations on $A_1$, $A_2$ and $A_3$, the final states will be $1111111$. In the second example: For $i \le 6$, we can just apply one operation on $A_2$, the final states will be $11111101$; For $i \ge 7$, we can apply operations on $A_1, A_3, A_4, A_6$, the final states will be $11111111$.

import sys readline = sys.stdin.readline class UF(): def __init__(self, num): self.par = [-1]*num self.weight = [0]*num def find(self, x): stack = [] while self.par[x] >= 0: stack.append(x) x = self.par[x] for xi in stack: self.par[xi] = x return x def union(self, x, y): rx = self.find(x) ry = self.find(y) if rx != ry: if self.par[rx] > self.par[ry]: rx, ry = ry, rx self.par[rx] += self.par[ry] self.par[ry] = rx self.weight[rx] += self.weight[ry] return rx N, K = list(map(int, readline().split())) S = list(map(int, readline().strip())) A = [[] for _ in range(N)] for k in range(K): BL = int(readline()) B = list(map(int, readline().split())) for b in B: A[b-1].append(k) cnt = 0 T = UF(2*K) used = set() Ans = [None]*N inf = 10**9+7 for i in range(N): if not len(A[i]): Ans[i] = cnt continue kk = 0 if len(A[i]) == 2: x, y = A[i] if S[i]: rx = T.find(x) ry = T.find(y) if rx != ry: rx2 = T.find(x+K) ry2 = T.find(y+K) sp = min(T.weight[rx], T.weight[rx2]) + min(T.weight[ry], T.weight[ry2]) if x not in used: used.add(x) T.weight[rx] += 1 if y not in used: used.add(y) T.weight[ry] += 1 rz = T.union(rx, ry) rz2 = T.union(rx2, ry2) sf = min(T.weight[rz], T.weight[rz2]) kk = sf - sp else: rx = T.find(x) ry2 = T.find(y+K) sp = 0 if rx != ry2: ry = T.find(y) rx2 = T.find(x+K) sp = min(T.weight[rx], T.weight[rx2]) + min(T.weight[ry], T.weight[ry2]) if x not in used: used.add(x) T.weight[rx] += 1 if y not in used: used.add(y) T.weight[ry] += 1 rz = T.union(rx, ry2) rz2 = T.union(rx2, ry) sf = min(T.weight[rz], T.weight[rz2]) kk = sf - sp else: if S[i]: x = A[i][0] rx = T.find(x) rx2 = T.find(x+K) sp = min(T.weight[rx], T.weight[rx2]) T.weight[rx] += inf sf = min(T.weight[rx], T.weight[rx2]) kk = sf - sp else: x = A[i][0] rx = T.find(x) rx2 = T.find(x+K) sp = min(T.weight[rx], T.weight[rx2]) T.weight[rx2] += inf if x not in used: used.add(x) T.weight[rx] += 1 sf = min(T.weight[rx], T.weight[rx2]) kk = sf-sp Ans[i] = cnt + kk cnt = Ans[i] print('\n'.join(map(str, Ans)))

train

APPS_structured

Chef loves lucky numbers. Everybody knows that lucky numbers are positive integers whose decimal representation contains only the lucky digits 4 and 7. For example, numbers 47, 744, 4 are lucky and 5, 17, 467 are not. Let F(X) equals to the number of lucky digits in decimal representation of X. Chef wants to know the number of such integers X, that L ≤ X ≤ R and F(X) is a lucky number. Help him and calculate that number modulo 109+7. -----Input----- First line contains one integer T, the number of test cases. Each of the following T lines contains two space separated positive integers L and R. -----Output----- For each of the T test cases print one integer, the number of such X, that L ≤ X ≤ R and F(X) is a lucky number, modulo 1000000007. -----Constraints----- 1 ≤ T ≤ 10 1 ≤ L ≤ R ≤ 101000 -----Example----- Input: 4 1 100 1 10000 1 100000 4444 4447 Output: 0 16 640 2 -----Notes----- First test case: of course, any number of less than 4 digits can't contain lucky number of lucky digits, so the answer is 0. Second test case: 16 required numbers are 4444 4447 4474 4477 4744 4747 4774 4777 7444 7447 7474 7477 7744 7747 7774 7777. Third test case: there are 640 required lucky numbers. Some of them are 4474, 14747, 41474, 77277, 44407, 74749. Fourth test case: the only two required numbers are 4444 and 4447.

lucky = {4, 774, 7, 744, 777, 74, 747, 44, 77, 47, 474, 444, 477, 447} from functools import lru_cache import sys sys.setrecursionlimit(10 ** 6) mod = 10 ** 9 + 7 fact = [1] for i in range(1, 1001): fact.append(fact[-1] * i % mod) inv = [pow(i, mod-2, mod) for i in fact] C = lambda k, n: fact[n] * inv[n-k] * inv[k] % mod def f(n): n = [int(x) for x in n] @lru_cache(None) def dp(pos, cnt, free): if cnt > 777: return 0 diff = len(n) - pos ans = 0 if free: for i in lucky: i -= cnt if 0 <= i <= diff: ans += C(i, diff) * pow(2, i, mod) * pow(8, diff - i, mod) ans %= mod return ans if pos == len(n): return int(cnt in lucky) for i in range(10 if free else n[pos]+1): ans += dp(pos+1, cnt + int(i == 4 or i == 7), free or i < n[pos]) ans %= mod return ans return dp(0, 0, 0) t = int(input()) for _ in range(t): l, r = input().split() l = str(int(l) -1) print((f(r) - f(l)) % mod)

train

APPS_structured

— Hey folks, how do you like this problem? — That'll do it. BThero is a powerful magician. He has got $n$ piles of candies, the $i$-th pile initially contains $a_i$ candies. BThero can cast a copy-paste spell as follows: He chooses two piles $(i, j)$ such that $1 \le i, j \le n$ and $i \ne j$. All candies from pile $i$ are copied into pile $j$. Formally, the operation $a_j := a_j + a_i$ is performed. BThero can cast this spell any number of times he wants to — but unfortunately, if some pile contains strictly more than $k$ candies, he loses his magic power. What is the maximum number of times BThero can cast the spell without losing his power? -----Input----- The first line contains one integer $T$ ($1 \le T \le 500$) — the number of test cases. Each test case consists of two lines: the first line contains two integers $n$ and $k$ ($2 \le n \le 1000$, $2 \le k \le 10^4$); the second line contains $n$ integers $a_1$, $a_2$, ..., $a_n$ ($1 \le a_i \le k$). It is guaranteed that the sum of $n$ over all test cases does not exceed $1000$, and the sum of $k$ over all test cases does not exceed $10^4$. -----Output----- For each test case, print one integer — the maximum number of times BThero can cast the spell without losing his magic power. -----Example----- Input 3 2 2 1 1 3 5 1 2 3 3 7 3 2 2 Output 1 5 4 -----Note----- In the first test case we get either $a = [1, 2]$ or $a = [2, 1]$ after casting the spell for the first time, and it is impossible to cast it again.

# ========== //\\ //|| ||====//|| # || // \\ || || // || # || //====\\ || || // || # || // \\ || || // || # ========== // \\ ======== ||//====|| # code def solve(): n, k = map(int, input().split()) a = list(map(int, input().split())) a.sort() ans = 0 for i in a[1:]: ans += (k - i) // a[0] print(ans) return def main(): t = 1 t = int(input()) for _ in range(t): solve() def __starting_point(): main() __starting_point()

train

APPS_structured

Your task is to write a function which counts the number of squares contained in an ASCII art picture. The input pictures contain rectangles---some of them squares---drawn with the characters `-`, `|`, and `+`, where `-` and `|` are used to represent horizontal and vertical sides, and `+` is used to represent corners and intersections. Each picture may contain multiple, possibly overlapping, rectangles. A simple example input looks like this: +--+ +----+ | | | | +-+ | | +----+ | | +--+ +-+ There are two squares and one rectangle in this picture, so your function should return 2 for this input. The following picture does not contain any squares, so the answer for this one is 0: +------+ | | +------+ Here is another, more complex input: +---+ | | | +-+-+ | | | | +-+-+ | | | +---+ The answer for this one is 3: two big squares, and a smaller square formed by the intersection of the two bigger ones. Similarly, the answer for the following picture is 5: +-+-+ | | | +-+-+ | | | +-+-+ You are going to implement a function `count_squares()` which takes an ASCII art picture as input and returns the number of squares the picture shows. The input to that function is an array of strings, where each string corresponds to a line of the ASCII art picture. Each string is guaranteed to contain only the characters `-`, `|`, `+`, and `` `` (space). The smallest valid square has a side length of 2 and is represented by four `+` characters arranged in a square; a single `+` character is not considered a square. Have fun!

import re def count_squares(shapes): squares = 0 for i, j in enumerate(shapes): ind = [k for k, l in enumerate(j) if l == '+'] for o in range(len(ind)): for p in range(o + 1, len(ind)): k, l = ind[o], ind[p] width = l - k if i + width >= len(shapes): continue upper_line = j[k:l + 1] left_line = ''.join([n[k] if k < len(n) else ' ' for n in shapes[i:i + width + 1]]) right_line = ''.join([n[l] if l < len(n) else ' ' for n in shapes[i:i + width + 1]]) bottom_line = shapes[i + width][k:l + 1] if all(re.fullmatch(r'\+[{}]*\+'.format(ch), seq) for seq, ch in \ zip([upper_line, left_line, right_line, bottom_line], '\+\- |\+ |\+ \-\+'.split())): squares += 1 return squares

train

APPS_structured

Given an Array and an Example-Array to sort to, write a function that sorts the Array following the Example-Array. Assume Example Array catalogs all elements possibly seen in the input Array. However, the input Array does not necessarily have to have all elements seen in the Example. Example: Arr: [1,3,4,4,4,4,5] Example Arr: [4,1,2,3,5] Result: [4,4,4,4,1,3,5]

def example_sort(arr, example_arr): return [a for e in example_arr for a in arr if a == e]

train

APPS_structured

Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum. Example: Input: [-2,1,-3,4,-1,2,1,-5,4], Output: 6 Explanation: [4,-1,2,1] has the largest sum = 6. Follow up: If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.

class Solution: def maxSubArray(self, nums): """ :type nums: List[int] :rtype: int """ # i = 0 # i_keep = 0 # j = 1 # j_keep = 1 # max_sum = nums[0]-1 # while j < len(nums) and i < j: # temp_sum = sum(nums[i:j]) # if temp_sum >= max_sum: # i_keep = i # j_keep = j # max_sum = temp_sum # elif i == j-1: # i += 1 # j += 1 # j += 1 # return max_sum # brute force # max_sum = nums[0] # for i in range(len(nums)): # for j in range(i,len(nums)+1): # temp_sum = sum(nums[i:j]) # if temp_sum > max_sum and i != j: # max_sum = temp_sum # return max_sum # outer loop only max_sum = csum = nums[0] for num in nums[1:]: if num >= csum + num: csum = num else: csum += num if csum > max_sum: max_sum = csum return max_sum

train

APPS_structured

Given 2 strings, `a` and `b`, return a string of the form: `shorter+reverse(longer)+shorter.` In other words, the shortest string has to be put as prefix and as suffix of the reverse of the longest. Strings `a` and `b` may be empty, but not null (In C# strings may also be null. Treat them as if they are empty.). If `a` and `b` have the same length treat `a` as the longer producing `b+reverse(a)+b`

def shorter_reverse_longer(a,b): return a+b[::-1]+a if len(b)>len(a) else b+a[::-1]+b

train

APPS_structured

There are N gas stations along a circular route, where the amount of gas at station i is gas[i]. You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from station i to its next station (i+1). You begin the journey with an empty tank at one of the gas stations. Return the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return -1. Note: If there exists a solution, it is guaranteed to be unique. Both input arrays are non-empty and have the same length. Each element in the input arrays is a non-negative integer. Example 1: Input: gas = [1,2,3,4,5] cost = [3,4,5,1,2] Output: 3 Explanation: Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4 Travel to station 4. Your tank = 4 - 1 + 5 = 8 Travel to station 0. Your tank = 8 - 2 + 1 = 7 Travel to station 1. Your tank = 7 - 3 + 2 = 6 Travel to station 2. Your tank = 6 - 4 + 3 = 5 Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3. Therefore, return 3 as the starting index. Example 2: Input: gas = [2,3,4] cost = [3,4,3] Output: -1 Explanation: You can't start at station 0 or 1, as there is not enough gas to travel to the next station. Let's start at station 2 and fill up with 4 unit of gas. Your tank = 0 + 4 = 4 Travel to station 0. Your tank = 4 - 3 + 2 = 3 Travel to station 1. Your tank = 3 - 3 + 3 = 3 You cannot travel back to station 2, as it requires 4 unit of gas but you only have 3. Therefore, you can't travel around the circuit once no matter where you start.

class Solution: def canCompleteCircuit(self, gas, cost): """ :type gas: List[int] :type cost: List[int] :rtype: int """ if sum(gas)< sum(cost): return -1 rest = 0 position = 0 for i in range(len(gas)): rest += gas[i]-cost[i] if rest < 0: rest = 0 position = i+1 return position

train

APPS_structured

Richik$Richik$ has just completed his engineering and has got a job in one of the firms at Sabrina$Sabrina$ which is ranked among the top seven islands in the world in terms of the pay scale. Since Richik$Richik$ has to travel a lot to reach the firm, the owner assigns him a number X$X$, and asks him to come to work only on the day which is a multiple of X$X$. Richik joins the firm on 1-st day but starts working from X-th day. Richik$Richik$ is paid exactly the same amount in Dollars as the day number. For example, if Richik$Richik$ has been assigned X=3$X = 3$, then he will be paid 3$3$ dollars and 6$6$ dollars on the 3rd$3rd$ and 6th$6th$ day on which he comes for work. On N−th$N-th$ day, the owner calls up Richik$Richik$ and asks him not to come to his firm anymore. Hence Richik$Richik$ demands his salary of all his working days together. Since it will take a lot of time to add, Richik$Richik$ asks help from people around him, let's see if you can help him out. -----Input:----- - First line will contain T$T$, number of testcases. Then the testcases follow. - Each testcase contains of a single line of input, two integers X,N$X, N$. -----Output:----- For each testcase, output in a single line which is the salary which Richik$Richik$ demands. -----Constraints----- - 1≤T≤1000$1 \leq T \leq 1000$ - 1≤X<=N≤107$1 \leq X<=N \leq 10^7$ -----Sample Input:----- 1 3 10 -----Sample Output:----- 18

for _ in range(int(input())): a,b=list(map(int,input().split())) i=a total=0 j=1 while b>i: total=total+a*j j+=1 i+=a print(total)

train

APPS_structured

LeetCode company workers use key-cards to unlock office doors. Each time a worker uses their key-card, the security system saves the worker's name and the time when it was used. The system emits an alert if any worker uses the key-card three or more times in a one-hour period. You are given a list of strings keyName and keyTime where [keyName[i], keyTime[i]] corresponds to a person's name and the time when their key-card was used in a single day. Access times are given in the 24-hour time format "HH:MM", such as "23:51" and "09:49". Return a list of unique worker names who received an alert for frequent keycard use. Sort the names in ascending order alphabetically. Notice that "10:00" - "11:00" is considered to be within a one-hour period, while "22:51" - "23:52" is not considered to be within a one-hour period. Example 1: Input: keyName = ["daniel","daniel","daniel","luis","luis","luis","luis"], keyTime = ["10:00","10:40","11:00","09:00","11:00","13:00","15:00"] Output: ["daniel"] Explanation: "daniel" used the keycard 3 times in a one-hour period ("10:00","10:40", "11:00"). Example 2: Input: keyName = ["alice","alice","alice","bob","bob","bob","bob"], keyTime = ["12:01","12:00","18:00","21:00","21:20","21:30","23:00"] Output: ["bob"] Explanation: "bob" used the keycard 3 times in a one-hour period ("21:00","21:20", "21:30"). Example 3: Input: keyName = ["john","john","john"], keyTime = ["23:58","23:59","00:01"] Output: [] Example 4: Input: keyName = ["leslie","leslie","leslie","clare","clare","clare","clare"], keyTime = ["13:00","13:20","14:00","18:00","18:51","19:30","19:49"] Output: ["clare","leslie"] Constraints: 1 <= keyName.length, keyTime.length <= 105 keyName.length == keyTime.length keyTime are in the format "HH:MM". [keyName[i], keyTime[i]] is unique. 1 <= keyName[i].length <= 10 keyName[i] contains only lowercase English letters.

class Solution: def alertNames(self, keyName: List[str], keyTime: List[str]) -> List[str]: keytime_table = dict() for idx in range(len(keyName)): name = keyName[idx] time = keyTime[idx] keytime_table.setdefault(name, []).append(time) ans = [] for name in list(keytime_table.keys()): time_list = keytime_table[name] time_list.sort() l = 0 r = 0 hour, minute = time_list[0].split(':') l_minutes = int(hour) * 60 + int(minute) while l <= r and r < len(time_list): r_time = time_list[r] hour, minute = r_time.split(':') r_minutes = int(hour) * 60 + int(minute) #print(l, r, name, time_list, l_minutes, r_minutes, ans) if r_minutes - l_minutes <= 60: if r - l >= 2: ans.append(name) break r += 1 else: l += 1 if l > r: r += 1 l_time = time_list[l] hour, minute = l_time.split(':') l_minutes = int(hour) * 60 + int(minute) ans.sort() return ans

train

APPS_structured

# Task You are a lifelong fan of your local football club, and proud to say you rarely miss a game. Even though you're a superfan, you still hate boring games. Luckily, boring games often end in a draw, at which point the winner is determined by a penalty shoot-out, which brings some excitement to the viewing experience. Once, in the middle of a penalty shoot-out, you decided to count the lowest total number of shots required to determine the winner. So, given the number of shots each team has already made and the current score, `how soon` can the game end? If you are not familiar with penalty shoot-out rules, here they are: `Teams take turns to kick from the penalty mark until each has taken five kicks. However, if one side has scored more successful kicks than the other could possibly reach with all of its remaining kicks, the shoot-out immediately ends regardless of the number of kicks remaining.` `If at the end of these five rounds of kicks the teams have scored an equal number of successful kicks, additional rounds of one kick each will be used until the tie is broken.` # Input/Output `[input]` integer `shots` An integer, the number of shots each team has made thus far. `0 ≤ shots ≤ 100.` `[input]` integer array `score` An array of two integers, where score[0] is the current score of the first team and score[1] - of the second team. `score.length = 2,` `0 ≤ score[i] ≤ shots.` `[output]` an integer The minimal possible total number of shots required to determine the winner. # Example For `shots = 2 and score = [1, 2]`, the output should be `3`. The possible 3 shots can be: ``` shot1: the first team misses the penalty shot2: the second team scores shot3: the first one misses again``` then, score will be [1, 3]. As the first team can't get 2 more points in the last remaining shot until the end of the initial five rounds, the winner is determined. For `shots = 10 and score = [10, 10]`, the output should be `2`. If one of the teams misses the penalty and the other one scores, the game ends.

def penaltyShots(shots, score): if shots >= 4 and score[0] == score[1]: return 2 elif shots >= 4 and abs(score[0]-score[1]) == 2: return 0 elif shots >= 4 and abs(score[0]-score[1]) == 1: return 1 elif shots >= 4 and ((score[0] or score[1]) == 3): return -1 elif shots >= 4 and ((score[0] or score[1]) == 4): return -2 else: if score[0] == score[1]: return 6-shots else: return 6 - (shots + abs(score[0]-score[1]))

train

APPS_structured

Consider the sequence `S(n, z) = (1 - z)(z + z**2 + z**3 + ... + z**n)` where `z` is a complex number and `n` a positive integer (n > 0). When `n` goes to infinity and `z` has a correct value (ie `z` is in its domain of convergence `D`), `S(n, z)` goes to a finite limit `lim` depending on `z`. Experiment with `S(n, z)` to guess the domain of convergence `D`of `S` and `lim` value when `z` is in `D`. Then determine the smallest integer `n` such that `abs(S(n, z) - lim) < eps` where `eps` is a given small real number and `abs(Z)` is the modulus or norm of the complex number Z. Call `f` the function `f(z, eps)` which returns `n`. If `z` is such that `S(n, z)` has no finite limit (when `z` is outside of `D`) `f` will return -1. # Examples: I is a complex number such as I * I = -1 (sometimes written `i` or `j`). `f(0.3 + 0.5 * I, 1e-4) returns 17` `f(30 + 5 * I, 1e-4) returns -1` # Remark: For languages that don't have complex numbers or "easy" complex numbers, a complex number `z` is represented by two real numbers `x` (real part) and `y` (imaginary part). `f(0.3, 0.5, 1e-4) returns 17` `f(30, 5, 1e-4) returns -1` # Note: You pass the tests if `abs(actual - exoected) <= 1`

import math def f(z, eps): return max(-1, math.log(eps)/math.log(math.hypot(z.real, z.imag)))

train

APPS_structured

Complete the method/function so that it converts dash/underscore delimited words into camel casing. The first word within the output should be capitalized **only** if the original word was capitalized (known as Upper Camel Case, also often referred to as Pascal case). ## Examples ```python to_camel_case("the-stealth-warrior") # returns "theStealthWarrior" to_camel_case("The_Stealth_Warrior") # returns "TheStealthWarrior" ```

def to_camel_case(text): words = text.replace('_', '-').split('-') return words[0] + ''.join([x.title() for x in words[1:]])

train

APPS_structured

# Back-Story Every day I travel on the freeway. When I am more bored than usual I sometimes like to play the following counting game I made up: * As I join the freeway my count is ```0``` * Add ```1``` for every car that I overtake * Subtract ```1``` for every car that overtakes me * Stop counting when I reach my exit What an easy game! What fun! # Kata Task You will be given * The distance to my exit (km) * How fast I am going (kph) * Information about a lot of other cars * Their time (relative to me) as I join the freeway. For example, * ```-1.5``` means they already passed my starting point ```1.5``` minutes ago * ```2.2``` means they will pass my starting point ```2.2``` minutes from now * How fast they are going (kph) Find what is my "score" as I exit the freeway! # Notes * Assume all cars travel at a constant speeds Safety Warning If you plan to play this "game" remember that it is not really a game. You are in a **real** car. There may be a temptation to try to beat your previous best score. Please don't do that...

def freeway_game(dist_km_to_exit, my_speed_kph, other_cars): score = 0 for pair in other_cars: if(my_speed_kph == pair[1]): continue if( 0 < pair[1]*(pair[0]/60) / (pair[1] - my_speed_kph) < dist_km_to_exit/my_speed_kph): score = score - 1 if pair[0] > 0 else score + 1 return score

train

APPS_structured

Kefaa has developed a novel decomposition of a tree. He claims that this decomposition solves many difficult problems related to trees. However, he doesn't know how to find it quickly, so he asks you to help him. You are given a tree with $N$ vertices numbered $1$ through $N$. Let's denote an edge between vertices $u$ and $v$ by $(u, v)$. The triple-tree decomposition is a partition of edges of the tree into unordered triples of edges $(a, b), (a, c), (a, d)$ such that $a \neq b \neq c \neq d$. Each edge must belong to exactly one triple. Help Kefaa with this problem — find a triple-tree decomposition of the given tree or determine that no such decomposition exists. -----Input----- - The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows. - The first line of each test case contains a single integer $N$. - Each of the following $N-1$ lines contains two space-separated integers $u$ and $v$ describing an edge between vertices $u$ and $v$ of the tree. -----Output----- - For each test case, print a line containing the string "YES" if a triple-tree decomposition of the given tree exists or "NO" otherwise. - If it exists, print $\frac{N-1}{3}$ more lines describing a decomposition. - Each of these lines should contain four space-separated integers $a$, $b$, $c$ and $d$ describing a triple of edges $(a, b), (a, c), (a, d)$. If more than one triple-tree decomposition exists, you may output any one. -----Constraints----- - $1 \le T \le 100$ - $2 \le N \le 2 \cdot 10^5$ - $1 \le u, v \le N$ - the sum of $N$ over all test cases does not exceed $2 \cdot 10^5$ -----Subtasks----- Subtask #1 (20 points): $2 \le N \le 10$ Subtask #2 (30 points):$2 \le N \le 5000$ and the sum of $N$ overall testcases doesn't exceed $5000$ Subtask #3 (50 points): original constraints -----Example Input----- 2 4 1 2 1 3 1 4 7 1 2 2 3 1 4 4 5 1 6 6 7 -----Example Output----- YES 1 2 3 4 NO

test=int(input()) for t in range(test): n= int(input()) adj=[[] for i in range(n+1)] for _ in range(n-1): a,b=list(map(int,input().split())) adj[a].append(b) adj[b].append(a) #print(adj) root=1 q,s=[root],set([root]) for x in q: adj[x]= [p for p in adj[x] if p not in s] q.extend(adj[x]) s.update(adj[x]) #print(adj) ans=True for i in range(n+1): if(len(adj[i]) %3!=0): ans=False if(ans): print("YES") for i in range(n+1): while(len(adj[i])): print(i,adj[i][0],adj[i][1],adj[i][2]) adj[i].pop(0) adj[i].pop(0) adj[i].pop(0) else: print("NO")

train

APPS_structured

Given a sequence of numbers, find the largest pair sum in the sequence. For example ``` [10, 14, 2, 23, 19] --> 42 (= 23 + 19) [99, 2, 2, 23, 19] --> 122 (= 99 + 23) ``` Input sequence contains minimum two elements and every element is an integer.

from heapq import nlargest def largest_pair_sum(a): return sum(nlargest(2, a))

train

APPS_structured

Recently Chef learned about Longest Increasing Subsequence. To be precise, he means longest strictly increasing subsequence, when he talks of longest increasing subsequence. To check his understanding, he took his favorite n-digit number and for each of its n digits, he computed the length of the longest increasing subsequence of digits ending with that digit. Then he stored these lengths in an array named LIS. For example, let us say that Chef's favourite 4-digit number is 1531, then the LIS array would be [1, 2, 2, 1]. The length of longest increasing subsequence ending at first digit is 1 (the digit 1 itself) and at the second digit is 2 ([1, 5]), at third digit is also 2 ([1, 3]), and at the 4th digit is 1 (the digit 1 itself). Now Chef wants to give you a challenge. He has a valid LIS array with him, and wants you to find any n-digit number having exactly the same LIS array? You are guaranteed that Chef's LIS array is valid, i.e. there exists at least one n-digit number corresponding to the given LIS array. -----Input----- The first line of the input contains an integer T denoting the number of test cases. For each test case, the first line contains an integer n denoting the number of digits in Chef's favourite number. The second line will contain n space separated integers denoting LIS array, i.e. LIS1, LIS2, ..., LISn. -----Output----- For each test case, output a single n-digit number (without leading zeroes) having exactly the given LIS array. If there are multiple n-digit numbers satisfying this requirement, any of them will be accepted. -----Constraints----- - 1 ≤ T ≤ 30 000 - 1 ≤ n ≤ 9 - It is guaranteed that at least one n-digit number having the given LIS array exists -----Example----- Input: 5 1 1 2 1 2 2 1 1 4 1 2 2 1 7 1 2 2 1 3 2 4 Output: 7 36 54 1531 1730418 -----Explanation----- Example case 1. All one-digit numbers have the same LIS array, so any answer from 0 to 9 will be accepted. Example cases 2 & 3. For a two digit number we always have LIS1 = 1, but the value of LIS2 depends on whether the first digit is strictly less than the second one. If this is the case (like for number 36), LIS2 = 2, otherwise (like for numbers 54 or 77) the values of LIS2 is 1. Example case 4. This has already been explained in the problem statement. Example case 5. 7-digit number 1730418 has LIS array [1, 2, 2, 1, 3, 2, 4]: indexLISlength117304181217304182317304182417304181517304183617304182717304184

for _ in range (int(input())) : n = int(input()) print(*list(map(int, input().split())), sep = '')

train

APPS_structured

Given an array arr of integers, check if there exists two integers N and M such that N is the double of M ( i.e. N = 2 * M). More formally check if there exists two indices i and j such that : i != j 0 <= i, j < arr.length arr[i] == 2 * arr[j] Example 1: Input: arr = [10,2,5,3] Output: true Explanation: N = 10 is the double of M = 5,that is, 10 = 2 * 5. Example 2: Input: arr = [7,1,14,11] Output: true Explanation: N = 14 is the double of M = 7,that is, 14 = 2 * 7. Example 3: Input: arr = [3,1,7,11] Output: false Explanation: In this case does not exist N and M, such that N = 2 * M. Constraints: 2 <= arr.length <= 500 -10^3 <= arr[i] <= 10^3

class Solution: def checkIfExist(self, arr: List[int]) -> bool: if len(arr) == 0 or len(arr) == 1: return False else: for i in range(len(arr) - 1): for j in range(i + 1, len(arr)): if arr[i] == 2 * arr[j] or arr[j] == 2 * arr[i]: return True return False

train

APPS_structured

Consider the following $4 \times 4$ pattern: 1 2 4 7 3 5 8 11 6 9 12 14 10 13 15 16 You are given an integer $N$. Print the $N \times N$ pattern of the same kind (containing integers $1$ through $N^2$). -----Input----- - The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows. - The first and only line of each test case contains a single integer $N$. -----Output----- For each test case, print $N$ lines; each of them should contain $N$ space-separated integers. -----Constraints----- - $1 \le T \le 10$ - $1 \le N \le 100$ -----Subtasks----- Subtask #1 (100 points): Original constraints -----Example Input----- 1 4 -----Example Output----- 1 2 4 7 3 5 8 11 6 9 12 14 10 13 15 16 -----Explanation-----

# cook your dish here try: for u in range(int(input())): n = int(input()) li = [] lid = [] a = 1 t = 0 l = 0 for i in range(n*n): t+=1 lid.append(i+1) if a == t: if l!=-1: a+=1 t = 0 else: a-=1 t = 0 li.append([int(k) for k in lid]) lid.clear() if a==n: l = -1 li2 = li.copy() for i in li: if len(li2)!=0: a = 0 li3 = li2.copy() for j in li2: if a == n: break a+=1 if len(j)!=0: print(j[0],end=" ") j.remove(j[0]) li2.clear() li2 = li3.copy() if len(j)!=0: print() else: break li2.remove(li2[0]) print() except: pass

train

APPS_structured

You've just recently been hired to calculate scores for a Dart Board game! Scoring specifications: * 0 points - radius above 10 * 5 points - radius between 5 and 10 inclusive * 10 points - radius less than 5 **If all radii are less than 5, award 100 BONUS POINTS!** Write a function that accepts an array of radii (can be integers and/or floats), and returns a total score using the above specification. An empty array should return 0. ## Examples:

def score_throws(radiuses): score = 0 for r in radiuses: if r < 5: score += 10 elif 5 <= r <= 10: score += 5 if radiuses and max(radiuses) < 5: score += 100 return score

train

APPS_structured

Your retro heavy metal band, VÄxën, originally started as kind of a joke, just because why would anyone want to use the crappy foosball table in your startup's game room when they could be rocking out at top volume in there instead? Yes, a joke, but now all the top tech companies are paying you top dollar to play at their conferences and big product-release events. And just as how in the early days of the Internet companies were naming everything "i"-this and "e"-that, now that VÄxënmänïä has conquered the tech world, any company that doesn't use Hëävÿ Mëtäl Ümläüts in ëvëry pössïblë pläcë is looking hopelessly behind the times. Well, with great power chords there must also come great responsibility! You need to help these companies out by writing a function that will guarantee that their web sites and ads and everything else will RÖCK ÄS MÜCH ÄS PÖSSÏBLË! Just think about it -- with the licensing fees you'll be getting from Gööglë, Fäcëböök, Äpplë, and Ämäzön alone, you'll probably be able to end world hunger, make college and Marshall stacks free to all, and invent self-driving bumper cars. Sö lët's gët röckïng and röllïng! Pëdal tö thë MËTÄL! Here's a little cheatsheet that will help you write your function to replace the so-last-year letters a-e-i-o-u-and-sometimes-y with the following totally rocking letters: ``` A = Ä = \u00c4 E = Ë = \u00cb I = Ï = \u00cf O = Ö = \u00d6 U = Ü = \u00dc Y = Ÿ = \u0178 a = ä = \u00e4 e = ë = \u00eb i = ï = \u00ef o = ö = \u00f6 u = ü = \u00fc y = ÿ = \u00ff ``` ### Python issues First, Python in the Codewars environment has some codec/encoding issues with extended ASCII codes like the umlaut-letters required above. With Python 2.7.6, when writing your solution you can just copy the above umlaut-letters (instead of the unicode sequences) and paste them into your code, but I haven't found something yet that will work for *both* 2.7.6 and 3.4.3 -- hopefully I will find something soon (answers/suggestions are welcome!), and hopefully that part will also be easier with other languages when I add them. Second, along the same lines, don't bother trying to use string translate() and maketrans() to solve this in Python 2.7.6, because maketrans will see the character-mapping strings as being different lengths. Use a different approach instead.

# -*- coding: utf-8 -*- def heavy_metal_umlauts(boring_text): d = {'A': 'Ä', 'O': 'Ö', 'a': 'ä', 'E': 'Ë', 'U': 'Ü', 'e': 'ë', 'u': 'ü', 'I': 'Ï', 'Y': 'Ÿ', 'i': 'ï', 'y': 'ÿ', 'o': 'ö'} return ''.join(i if i not in d else d[i] for i in boring_text)

train

APPS_structured

Chef's dog Snuffles has so many things to play with! This time around, Snuffles has an array A containing N integers: A1, A2, ..., AN. Bad news: Snuffles only loves to play with an array in which all the elements are equal. Good news: We have a mover of size D. ! A mover of size D is a tool which helps to change arrays. Chef can pick two existing elements Ai and Aj from the array, such that i + D = j and subtract 1 from one of these elements (the element should have its value at least 1), and add 1 to the other element. In effect, a single operation of the mover, moves a value of 1 from one of the elements to the other. Chef wants to find the minimum number of times she needs to use the mover of size D to make all the elements of the array A equal. Help her find this out. -----Input----- - The first line of the input contains an integer T, denoting the number of test cases. The description of T test cases follows. - The first line of each test case contains two integers N and D, denoting the number of elements in the array and the size of the mover. - The second line of each testcase contains N space-separated integers: A1, A2, ..., AN, denoting the initial elements of the array. -----Output----- - For each test case, output a single line containing the minimum number of uses or -1 if it is impossible to do what Snuffles wants. -----Constraints----- - 1 ≤ T ≤ 10 - 2 ≤ N ≤ 105 - 1 ≤ D < N - 1 ≤ Ai ≤ 109 -----Subtasks----- - Subtask 1 (30 points) : N ≤ 103 - Subtask 2 (70 points) : Original constraints -----Example----- Input: 3 5 2 1 4 5 2 3 3 1 1 4 1 4 2 3 4 3 5 Output: 3 2 -1 -----Explanation----- Testcase 1: Here is a possible sequence of usages of the mover: - Move 1 from A3 to A1 - Move 1 from A3 to A1 - Move 1 from A2 to A4 At the end, the array becomes (3, 3, 3, 3, 3), which Snuffles likes. And you cannot achieve this in fewer moves. Hence the answer is 3. Testcase 2: Here is a possible sequence of usages of the mover: - Move 1 from A2 to A1 - Move 1 from A2 to A3 At the end, the array becomes (2, 2, 2), which Snuffles likes. And you cannot achieve this in fewer moves. Hence the answer is 2. Testcase 3: It is impossible to make all the elements equal. Hence the answer is -1.

t = int(input()) while t!=0: n,d=list(map(int,input().strip().split())) a=input().strip() a= a.split() c=0 b=[] c=sum(int(i) for i in a) if c%n!=0: print('-1') else: m=0 b += n*[c/n] f=1 for i in range(0,len(a)-d): if a.count(a[0]) == len(a): f=0 break else: if int(a[i])>int(b[i]): temp=int(a[i])-int(b[i]) a[i]=int(b[i]) a[i+d]=int(a[i+d])+temp m=m+temp elif int(a[i])<int(b[i]): temp=int(b[i])-int(a[i]) a[i]=int(b[i]) a[i+d]=int(a[i+d])-temp m=m+temp if i==(len(a)-d-1) and all(int(x)==int(a[0]) for x in a): f=0 if f==0: print(m) else: print('-1') t=t-1

train

APPS_structured

You are given 2 numbers is `n` and `k`. You need to find the number of integers between 1 and n (inclusive) that contains exactly `k` non-zero digit. Example1 ` almost_everywhere_zero(100, 1) return 19` by following condition we have 19 numbers that have k = 1 digits( not count zero ) ` [1,2,3,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100]` Example2 ` almost_everywhere_zero(11, 2) return 1` we have only `11` that has 2 digits(ten not count because zero is not count) ` 11` constrains `1≤n<pow(10,100)` `1≤k≤100`

from scipy.special import comb def almost_everywhere_zero(n, k): if k == 0: return 1 first, *rest = str(n) l = len(rest) return 9**k*comb(l, k, exact=True) +\ (int(first)-1)*9**(k-1)*comb(l, k-1, exact=True) +\ almost_everywhere_zero(int("".join(rest) or 0), k-1)

train

APPS_structured

A variation of determining leap years, assuming only integers are used and years can be negative and positive. Write a function which will return the days in the year and the year entered in a string. For example 2000, entered as an integer, will return as a string 2000 has 366 days There are a few assumptions we will accept the year 0, even though there is no year 0 in the Gregorian Calendar. Also the basic rule for validating a leap year are as follows Most years that can be divided evenly by 4 are leap years. Exception: Century years are NOT leap years UNLESS they can be evenly divided by 400. So the years 0, -64 and 2016 will return 366 days. Whilst 1974, -10 and 666 will return 365 days.

def year_days(year): if year % 4 != 0 : return f'{year} has {365} days' elif year % 4 == 0 and year % 100 == 0 and year % 400 != 0: return f'{year} has {365} days' else: return f'{year} has {366} days'

train

APPS_structured

You can print your name on a billboard ad. Find out how much it will cost you. Each letter has a default price of £30, but that can be different if you are given 2 parameters instead of 1. You can not use multiplier "*" operator. If your name would be Jeong-Ho Aristotelis, ad would cost £600. 20 leters * 30 = 600 (Space counts as a letter).

def billboard(name, price=30): cout = 0 for letters in name: cout += price return cout #your code here - note that in Python we cannot prevent the use of the #multiplication, but try not to be lame and solve the kata in another way!

train

APPS_structured

In this kata, you will be given a string of text and valid parentheses, such as `"h(el)lo"`. You must return the string, with only the text inside parentheses reversed, so `"h(el)lo"` becomes `"h(le)lo"`. However, if said parenthesized text contains parenthesized text itself, then that too must reversed back, so it faces the original direction. When parentheses are reversed, they should switch directions, so they remain syntactically correct (i.e. `"h((el)l)o"` becomes `"h(l(el))o"`). This pattern should repeat for however many layers of parentheses. There may be multiple groups of parentheses at any level (i.e. `"(1) (2 (3) (4))"`), so be sure to account for these. For example: ```python reverse_in_parentheses("h(el)lo") == "h(le)lo" reverse_in_parentheses("a ((d e) c b)") == "a (b c (d e))" reverse_in_parentheses("one (two (three) four)") == "one (ruof (three) owt)" reverse_in_parentheses("one (ruof ((rht)ee) owt)") == "one (two ((thr)ee) four)" ``` Input parentheses will always be valid (i.e. you will never get "(()").

def reverse_in_parentheses(string): a = 0 for n in range(string.count("(")): a, b = string.find("(", a), 0 for i in range(a, len(string)): if string[i] == "(": b += 1 elif string[i] == ")": b -= 1 if b == 0: break a += 1 string = string[:a] + string[a:i][::-1].translate(str.maketrans(")(", "()")) + string[i:] return string

train

APPS_structured

Santa is coming to town and he needs your help finding out who's been naughty or nice. You will be given an entire year of JSON data following this format: Your function should return `"Naughty!"` or `"Nice!"` depending on the total number of occurrences in a given year (whichever one is greater). If both are equal, return `"Nice!"`

def naughty_or_nice(data): nice_count = 0 naughty_count = 0 for month, days in data.items(): for date, status in days.items(): if status == 'Nice': nice_count += 1 else: naughty_count += 1 return 'Naughty!' if nice_count < naughty_count else 'Nice!'

train

APPS_structured

In Chefland, there is a monthly robots competition. In the competition, a grid table of N rows and M columns will be used to place robots. A cell at row i and column j in the table is called cell (i, j). To join this competition, each player will bring two robots to compete and each robot will be placed at a cell in the grid table. Both robots will move at the same time from one cell to another until they meet at the same cell in the table. Of course they can not move outside the table. Each robot has a movable range. If a robot has movable range K, then in a single move, it can move from cell (x, y) to cell (i, j) provided (|i-x| + |j-y| <= K). However, there are some cells in the table that the robots can not stand at, and because of that, they can not move to these cells. The two robots with the minimum number of moves to be at the same cell will win the competition. Chef plans to join the competition and has two robots with the movable range K1 and K2, respectively. Chef does not know which cells in the table will be used to placed his 2 robots, but he knows that there are 2 cells (1, 1) and (1, M) that robots always can stand at. Therefore, he assumes that the first robot is at cell (1, 1) and the other is at cell (1, M). Chef wants you to help him to find the minimum number of moves that his two robots needed to be at the same cell and promises to give you a gift if he wins the competition. -----Input----- The first line of the input contains an integer T denoting the number of test cases. The description of T test cases follows. - The first line of each test case contains 4 space-separated integers N M K1 K2 denoting the number of rows and columns in the table and the movable ranges of the first and second robot of Chef. - The next N lines, each line contains M space-separated numbers either 0 or 1 denoting whether the robots can move to this cell or not (0 means robots can move to this cell, 1 otherwise). It makes sure that values in cell (1, 1) and cell (1, M) are 0. -----Output----- For each test case, output a single line containing the minimum number of moves that Chef’s 2 robots needed to be at the same cell. If they can not be at the same cell, print -1. -----Constraints----- - 1 ≤ T ≤ 10 - 1 ≤ N, M ≤ 100 - 0 ≤ K1, K2 ≤ 10 ----- Subtasks ----- Subtask #1 : (25 points) - K1 = K2 = 1 Subtask # 2 : (75 points) Original Constraints -----Example----- Input: 2 4 4 1 1 0 1 1 0 0 1 1 0 0 1 1 0 0 0 0 0 4 4 1 1 0 1 1 0 0 1 1 0 0 1 1 0 1 0 0 1 Output: 5 -1 -----Explanation----- Example case 1. Robot 1 can move (1, 1) -> (2, 1) -> (3, 1) -> (4, 1) -> (4, 2) -> (4, 3), and robot 2 can move (1, 4) -> (2, 4) -> (3, 4) -> (4, 4) -> (4, 3) -> (4, 3), they meet at cell (4, 3) after 5 moves. Example case 2. Because the movable range of both robots is 1, robot 1 can not move from (3, 1) to (4, 2), and robot 2 can not move from (3, 4) to (4, 3. Hence, they can not meet each other.

import sys def spaces(a,n,m,k,visit1,visit2,dist,position): queue = [position] lastedit = [] dist[position[0]][position[1]] = 0 while queue!=[]: point = queue[0] i = point[0] j = point[1] #print 'point',i,j if visit1[i][j]==False: visit1[i][j] = True startx = max(i-k,0) endx = min(i+k,n-1) for x in range(startx,endx+1): starty = max(0,j+abs(x-i)-k) endy = min(m-1,j-abs(x-i)+k) for y in range(starty,endy+1): if (a[x][y]==0 and visit1[x][y]==False): if visit2[x][y]==True: lastedit.append([x,y]) #print x,y, if dist[x][y]>dist[i][j]+1: dist[x][y]=dist[i][j]+1 queue.append([x,y]) #print queue,dist queue = queue[1:] #print return lastedit for t in range(int(input())): n,m,k1,k2 = list(map(int,input().split())) a = [] for i in range(n): a.append(list(map(int,input().split()))) #print a value = sys.maxsize listing = [] visit1 = [[False for i in range(m)]for j in range(n)] visit2 = [[False for i in range(m)]for j in range(n)] dist1 = [[sys.maxsize for i in range(m)]for j in range(n)] dist2 = [[sys.maxsize for i in range(m)]for j in range(n)] if k1>=k2: spaces(a,n,m,k1,visit1,visit2,dist1,[0,0]) else: spaces(a,n,m,k2,visit1,visit2,dist1,[0,m-1]) listing = spaces(a,n,m,k1,visit2,visit1,dist2,[0,0]) if k1>k2: listing = spaces(a,n,m,k2,visit2,visit1,dist2,[0,m-1]) #print visit1 #sprint visit2 if k1==k2: if dist1[0][m-1]==sys.maxsize: print('-1') else: print(int((dist1[0][m-1]+1)/2)) else: d = len(listing) for i in range(d-1,-1,-1): x = listing[i][0] y = listing[i][1] if visit1[x][y]==True and dist2[x][y]<value: value = dist2[x][y] if value!=sys.maxsize: print(value) else: print('-1')

train

APPS_structured

You probably know that the "mode" of a set of data is the data point that appears most frequently. Looking at the characters that make up the string `"sarsaparilla"` we can see that the letter `"a"` appears four times, more than any other letter, so the mode of `"sarsaparilla"` is `"a"`. But do you know what happens when two or more data points occur the most? For example, what is the mode of the letters in `"tomato"`? Both `"t"` and `"o"` seem to be tied for appearing most frequently. Turns out that a set of data can, in fact, have multiple modes, so `"tomato"` has two modes: `"t"` and `"o"`. It's important to note, though, that if *all* data appears the same number of times there is no mode. So `"cat"`, `"redder"`, and `[1, 2, 3, 4, 5]` do not have a mode. Your job is to write a function `modes()` that will accept one argument `data` that is a sequence like a string or a list of numbers and return a sorted list containing the mode(s) of the input sequence. If data does not contain a mode you should return an empty list. For example: ```python >>> modes("tomato") ["o", "t"] >>> modes([1, 3, 3, 7]) [3] >>> modes(["redder"]) [] ``` You can trust that your input data will always be a sequence and will always contain orderable types (no inputs like `[1, 2, 2, "a", "b", "b"]`).

from collections import Counter def modes(data): count = Counter(data) m = max(count.values()) if len(set(count.values())) > 1 else 0 return sorted(item for item, number in count.items() if 0 < m == number)

train

APPS_structured

Remove the parentheses = In this kata you are given a string for example: ```python "example(unwanted thing)example" ``` Your task is to remove everything inside the parentheses as well as the parentheses themselves. The example above would return: ```python "exampleexample" ``` Other than parentheses only letters and spaces can occur in the string. Don't worry about other brackets like ```"[]"``` and ```"{}"``` as these will never appear.

import re def remove_parentheses(s): ret, count = "", 0 for letter in s: if letter == "(": count +=1 elif letter == ")": count -=1 elif count == 0: ret += letter return ret

train

APPS_structured

Given a binary tree root, a node X in the tree is named good if in the path from root to X there are no nodes with a value greater than X. Return the number of good nodes in the binary tree. Example 1: Input: root = [3,1,4,3,null,1,5] Output: 4 Explanation: Nodes in blue are good. Root Node (3) is always a good node. Node 4 -> (3,4) is the maximum value in the path starting from the root. Node 5 -> (3,4,5) is the maximum value in the path Node 3 -> (3,1,3) is the maximum value in the path. Example 2: Input: root = [3,3,null,4,2] Output: 3 Explanation: Node 2 -> (3, 3, 2) is not good, because "3" is higher than it. Example 3: Input: root = [1] Output: 1 Explanation: Root is considered as good. Constraints: The number of nodes in the binary tree is in the range [1, 10^5]. Each node's value is between [-10^4, 10^4].

# Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right class Solution: def goodNodes(self, root: TreeNode) -> int: def dfs(root, mval): if not root: return 0 l = dfs(root.left, root.val if root.val > mval else mval) r = dfs(root.right, root.val if root.val > mval else mval) return l + r + (1 if root.val >= mval else 0) return dfs(root, float(\"-inf\"))

train

APPS_structured

Apparently "Put A Pillow On Your Fridge Day is celebrated on the 29th of May each year, in Europe and the U.S. The day is all about prosperity, good fortune, and having bit of fun along the way." All seems very weird to me. Nevertheless, you will be given an array of two strings (s). First find out if the first string contains a fridge... (i've deemed this as being 'n', as it looks like it could hold something). Then check that the second string has a pillow - deemed 'B' (struggled to get the obvious pillow-esque character). If the pillow is on top of the fridge - it must be May 29th! Or a weird house... Return true; For clarity, on top means right on top, ie in the same index position. If the pillow is anywhere else in the 'house', return false; There may be multiple fridges, and multiple pillows. But you need at least 1 pillow ON TOP of a fridge to return true. Multiple pillows on fridges should return true also. 100 random tests

def pillow(s): return ('n', 'B') in zip(s[0],s[1])

train

APPS_structured

The chef is trying to solve some pattern problems, Chef wants your help to code it. Chef has one number K to form a new pattern. Help the chef to code this pattern problem. -----Input:----- - First-line will contain $T$, the number of test cases. Then the test cases follow. - Each test case contains a single line of input, one integer $K$. -----Output:----- For each test case, output as the pattern. -----Constraints----- - $1 \leq T \leq 100$ - $1 \leq K \leq 100$ -----Sample Input:----- 4 1 2 3 4 -----Sample Output:----- 2 24 68 246 81012 141618 2468 10121416 18202224 26283032 -----EXPLANATION:----- No need, else pattern can be decode easily.

# cook your dish here for _ in range(int(input())): k = int(input()) s = "" count = 1 for i in range(k): for j in range(k): s += str(count*2) count += 1 print(s) s = ""

train

APPS_structured

Every non-negative integer N has a binary representation. For example, 5 can be represented as "101" in binary, 11 as "1011" in binary, and so on. Note that except for N = 0, there are no leading zeroes in any binary representation. The complement of a binary representation is the number in binary you get when changing every 1 to a 0 and 0 to a 1. For example, the complement of "101" in binary is "010" in binary. For a given number N in base-10, return the complement of it's binary representation as a base-10 integer. Example 1: Input: 5 Output: 2 Explanation: 5 is "101" in binary, with complement "010" in binary, which is 2 in base-10. Example 2: Input: 7 Output: 0 Explanation: 7 is "111" in binary, with complement "000" in binary, which is 0 in base-10. Example 3: Input: 10 Output: 5 Explanation: 10 is "1010" in binary, with complement "0101" in binary, which is 5 in base-10. Note: 0 <= N < 10^9 This question is the same as 476: https://leetcode.com/problems/number-complement/

class Solution: def bitwiseComplement(self, N: int) -> int: if N==0: return 1 dummy_num=N n=0 while(dummy_num): n+=1 dummy_num>>=1 ans=0 for i in range(n-1,-1,-1): if (N>>i)&1==0: ans|=(1<<i) return ans

train

APPS_structured

One day, Chef found a cube which has each of its sides painted in some color out of black, blue, red, green, yellow and orange. Now he asks you to check if he can choose three sides such that they are pairwise adjacent and painted in the same color. -----Input----- - The first line of the input contains an integer T denoting the number of test cases. - A single line of each test case contains six words denoting the colors of painted sides in the order: front, back, left, right, top and bottom, respectively. -----Output----- For each test case, output a single line containing the word "YES" or "NO" (without quotes) corresponding to the answer of the problem. -----Constraints----- - 1 ≤ T ≤ 50000 - Each color will be from the list {"black", "blue", "red", "green", "yellow", "orange"} -----Subtasks----- Subtask 1: (25 points) - 1 ≤ T ≤ 12000 - For each test case there will be at most three different colors Subtask 2: (75 points) - Original constraints -----Example----- Input: 2 blue yellow green orange black green green yellow green orange black green Output: NO YES -----Explanation----- Example case 1. There are no three sides with the same color. Example case 2. In this test case, the front, bottom and left sides are green (see picture).

for _ in range(int(input())): l=list(map(str,input().split())) a=[(1,3,5),(1,3,6),(1,4,5),(1,4,6),(2,3,5),(2,3,6),(2,4,5),(2,4,6)] c=0 for i in a: if len(set([l[i[0]-1],l[i[1]-1],l[i[2]-1]]))==1: c=1 break if c==1: print("YES") else: print("NO")

train

APPS_structured

In this Kata, we will calculate the **minumum positive number that is not a possible sum** from a list of positive integers. ``` solve([1,2,8,7]) = 4 => we can get 1, 2, 3 (from 1+2), but we cannot get 4. 4 is the minimum number not possible from the list. solve([4,1,2,3,12]) = 11. We can get 1, 2, 3, 4, 4+1=5, 4+2=6,4+3=7,4+3+1=8,4+3+2=9,4+3+2+1=10. But not 11. solve([2,3,2,3,4,2,12,3]) = 1. We cannot get 1. ``` More examples in test cases. Good luck!

def solve(a): a.sort() i,j= 1,0 while j < len(a): j += 1 if a[j-1] <= i: i += a[j-1] else: break return i

train

APPS_structured

In this Kata, you will check if it is possible to convert a string to a palindrome by changing one character. For instance: ```Haskell solve ("abbx") = True, because we can convert 'x' to 'a' and get a palindrome. solve ("abba") = False, because we cannot get a palindrome by changing any character. solve ("abcba") = True. We can change the middle character. solve ("aa") = False solve ("ab") = True ``` Good luck! Please also try [Single Character Palindromes](https://www.codewars.com/kata/5a2c22271f7f709eaa0005d3)

def solve(s): print(s) if s == s[::-1] and len(s) % 2 == 0: return False left, right = [], [] l = list(s) counter = 0 while l: e = l.pop(0) if l: e2 = l.pop() if e != e2 and counter == 0: e2 = e counter += 1 right.insert(0, e2) else: e = left[-1] left.append(e) s = ''.join(left + right) return s == s[::-1]

train

APPS_structured

You are given two sorted arrays that contain only integers. Your task is to find a way to merge them into a single one, sorted in **ascending order**. Complete the function `mergeArrays(arr1, arr2)`, where `arr1` and `arr2` are the original sorted arrays. You don't need to worry about validation, since `arr1` and `arr2` must be arrays with 0 or more Integers. If both `arr1` and `arr2` are empty, then just return an empty array. **Note:** `arr1` and `arr2` may be sorted in different orders. Also `arr1` and `arr2` may have same integers. Remove duplicated in the returned result. ## Examples Happy coding!

def merge_arrays(arr1, arr2): arr1 = arr1+arr2 res = [] for i in arr1: if i not in res: res.append(i) return sorted(res)

train

APPS_structured

You are given a string containing only 4 kinds of characters 'Q', 'W', 'E' and 'R'. A string is said to be balanced if each of its characters appears n/4 times where n is the length of the string. Return the minimum length of the substring that can be replaced with any other string of the same length to make the original string s balanced. Return 0 if the string is already balanced. Example 1: Input: s = "QWER" Output: 0 Explanation: s is already balanced. Example 2: Input: s = "QQWE" Output: 1 Explanation: We need to replace a 'Q' to 'R', so that "RQWE" (or "QRWE") is balanced. Example 3: Input: s = "QQQW" Output: 2 Explanation: We can replace the first "QQ" to "ER". Example 4: Input: s = "QQQQ" Output: 3 Explanation: We can replace the last 3 'Q' to make s = "QWER". Constraints: 1 <= s.length <= 10^5 s.length is a multiple of 4 s contains only 'Q', 'W', 'E' and 'R'.

class Solution: def balancedString(self, s: str) -> int: # minimum window so that outside is possible if len(s) //4 != len(s) / 4: return -1 ans, p1, p2, n_cnt = len(s), 0, 0, collections.Counter(s) while p1 < len(s): n_cnt[s[p1]] -= 1 while p2 < len(s) and all(len(s) / 4 >= n_cnt[c] for c in 'QWER'): ans = min(ans, abs(p1 - p2 + 1)) n_cnt[s[p2]] += 1 p2 += 1 if p2 > p1: p1, p2 = p2, p1 p1 +=1 return ans

train

APPS_structured

We write the integers of A and B (in the order they are given) on two separate horizontal lines. Now, we may draw connecting lines: a straight line connecting two numbers A[i] and B[j] such that: A[i] == B[j]; The line we draw does not intersect any other connecting (non-horizontal) line. Note that a connecting lines cannot intersect even at the endpoints: each number can only belong to one connecting line. Return the maximum number of connecting lines we can draw in this way. Example 1: Input: A = [1,4,2], B = [1,2,4] Output: 2 Explanation: We can draw 2 uncrossed lines as in the diagram. We cannot draw 3 uncrossed lines, because the line from A[1]=4 to B[2]=4 will intersect the line from A[2]=2 to B[1]=2. Example 2: Input: A = [2,5,1,2,5], B = [10,5,2,1,5,2] Output: 3 Example 3: Input: A = [1,3,7,1,7,5], B = [1,9,2,5,1] Output: 2 Note: 1 <= A.length <= 500 1 <= B.length <= 500 1 <= A[i], B[i] <= 2000

class Solution: def maxUncrossedLines(self, A: List[int], B: List[int]) -> int: a = len(A) b = len(B) memo = {} for i in range(a): for j in range(b): if A[i] == B[j]: memo[(i,j)] = memo.get((i-1, j-1), 0) + 1 else: memo[(i,j)] = max(memo.get((i-1,j), 0), memo.get((i,j-1), 0)) return memo.get((a-1, b-1), 0)

train

APPS_structured

You have to write two methods to *encrypt* and *decrypt* strings. Both methods have two parameters: ``` 1. The string to encrypt/decrypt 2. The Qwerty-Encryption-Key (000-999) ``` The rules are very easy: ``` The crypting-regions are these 3 lines from your keyboard: 1. "qwertyuiop" 2. "asdfghjkl" 3. "zxcvbnm,." If a char of the string is not in any of these regions, take the char direct in the output. If a char of the string is in one of these regions: Move it by the part of the key in the region and take this char at the position from the region. If the movement is over the length of the region, continue at the beginning. The encrypted char must have the same case like the decrypted char! So for upperCase-chars the regions are the same, but with pressed "SHIFT"! The Encryption-Key is an integer number from 000 to 999. E.g.: 127 The first digit of the key (e.g. 1) is the movement for the first line. The second digit of the key (e.g. 2) is the movement for the second line. The third digit of the key (e.g. 7) is the movement for the third line. (Consider that the key is an integer! When you got a 0 this would mean 000. A 1 would mean 001. And so on.) ``` You do not need to do any prechecks. The strings will always be not null and will always have a length > 0. You do not have to throw any exceptions. An Example: ``` Encrypt "Ball" with key 134 1. "B" is in the third region line. Move per 4 places in the region. -> ">" (Also "upperCase"!) 2. "a" is in the second region line. Move per 3 places in the region. -> "f" 3. "l" is in the second region line. Move per 3 places in the region. -> "d" 4. "l" is in the second region line. Move per 3 places in the region. -> "d" --> Output would be ">fdd" ``` *Hint: Don't forget: The regions are from an US-Keyboard!* *In doubt google for "US Keyboard."* This kata is part of the Simple Encryption Series: Simple Encryption #1 - Alternating Split Simple Encryption #2 - Index-Difference Simple Encryption #3 - Turn The Bits Around Simple Encryption #4 - Qwerty Have fun coding it and please don't forget to vote and rank this kata! :-)

encrypt = lambda s, k: code(s, k) decrypt = lambda s, k: code(s, k, -1) def code(text, key, m=1): keys, r = [int(e) * m for e in str(key).rjust(3, '0')], [] for c in text: for i, a in enumerate(['qwertyuiop', 'asdfghjkl', 'zxcvbnm,.']): if c in a: c = a[(a.index(c) + keys[i]) % len(a)] for i, a in enumerate(['QWERTYUIOP', 'ASDFGHJKL', 'ZXCVBNM<>']): if c in a: c = a[(a.index(c) + keys[i]) % len(a)] r.append(c) return ''.join(r)

train

APPS_structured

Given two strings S and T, return if they are equal when both are typed into empty text editors. # means a backspace character. Note that after backspacing an empty text, the text will continue empty. Example 1: Input: S = "ab#c", T = "ad#c" Output: true Explanation: Both S and T become "ac". Example 2: Input: S = "ab##", T = "c#d#" Output: true Explanation: Both S and T become "". Example 3: Input: S = "a##c", T = "#a#c" Output: true Explanation: Both S and T become "c". Example 4: Input: S = "a#c", T = "b" Output: false Explanation: S becomes "c" while T becomes "b". Note: 1 <= S.length <= 200 1 <= T.length <= 200 S and T only contain lowercase letters and '#' characters. Follow up: Can you solve it in O(N) time and O(1) space?

class Solution: def backspaceCompare(self, S: str, T: str) -> bool: def helper(S): r = '' erase = 0 for s in S[-1::-1]: if s == '#': erase+=1 elif s !='#' and erase == 0: r=s+r elif s !='#' and erase >=1: #r=s+r erase-=1 return r return helper(S) == helper(T)

train

APPS_structured

Chef likes to travel a lot. Every day Chef tries to visit as much cities as possible. Recently he had a quite a few trips of great Chefland for learning various recipes. Chefland had N cities numbered from 1 to N. People in Chefland are very friendly, friendliness of i-th city is given by Fi. Before starting of each trip, Chef's initial enjoyment is 1 unit. Whenever he visits a city with friendliness Fi, his enjoyment gets multiplied by Fi units. City 1 is the home city of Chef. He starts each trip from his home city. Before starting a trip, he chooses a parameter R which denotes that he will start from city 1, and go to city 1 + R, then to 1 + 2 * R, then to 1 + 3 * R, till 1 + i * R such that i is largest integer satisfying 1 + i * R ≤ N. Now, Chef wants you to help him recreate his visit of the cities. Specifically, he will ask you Q queries, each of which can be of following two types. - 1 p f : friendliness of p-th city changes to f, i.e. Fp = f - 2 R : Find out the total enjoyment Chef will have during this trip. As Chef does not like big numbers, he just asks you to output two things, first digit of the enjoyment and value of enjoyment modulo 109 + 7. -----Input----- There is a single test case. First line of input contains a single integer N, denoting number of cities in Chefland. Second line of the input contains N space separated integer - F1, F2, ..., FN, denoting the friendliness of the cities in order from 1 to N. Next line contains an integer Q, denoting number of queries. For each of the next Q queries, each line corresponds to one of the two types of the query. First there will be an integer denoting the type of the query, followed by the actual query. For query of type 1, there will be three space separated integers "1 p f" as defined above. For query of type 2, there will be two space separated integers "2 R ", as defined above. -----Output----- For each query of type 2, output two space separated integers, first digit of Chef's enjoyment in this trip followed by the value of enjoyment modulo 109 + 7. -----Constraints----- - 1 ≤ N, Q ≤ 105 - 1 ≤ Fi ≤ 10^9 - 1 ≤ f ≤ 10^9 - 1 ≤ p ≤ N - 1 ≤ R ≤ N -----Subtasks----- Subtask #1 (5 points) : - 1 ≤ N ≤ 10 - 1 ≤ Q ≤ 1000 - 1 ≤ Fi ≤ 10 - 1 ≤ f ≤ 10 Subtask #2 (15 points) : - 1 ≤ N ≤ 1000 - 1 ≤ Q ≤ 100 - 1 ≤ Fi ≤ 109 - 1 ≤ f ≤ 1000 Subtask #3 (80 points) : - original constraints -----Example----- Input: 5 1 2 3 4 5 3 2 1 1 3 10 2 2 Output: 1 120 5 50 -----Explanation----- In the first query, Chef is going to visit cities 1, 2, 3, 4, 5 in order. At the end of the trip, his total enjoyment will be 1 * 2 * 3 * 4 * 5 = 120. First digit of enjoyment is 1 and 120 modulo 109 + 7 is 120. In the third query, Chef is going to visit cities 1, 3, 5 in order. At the end of the trip, his total enjoyment will be 1 * 10 * 5 = 50.

M = 10**9 + 7 n = int(input()) f = list(map(int, input().split())) q = int(input()) for i in range(q): query = input().split() if query[0] == '1': f[int(query[1]) -1] = int(query[2]) else: r = int(query[1]) k = 0 ans = 1 while k<n: ans *= f[k] k += r print(str(ans)[0], ans % M)

train

APPS_structured

Vanya wants to minimize a tree. He can perform the following operation multiple times: choose a vertex v, and two disjoint (except for v) paths of equal length a_0 = v, a_1, ..., a_{k}, and b_0 = v, b_1, ..., b_{k}. Additionally, vertices a_1, ..., a_{k}, b_1, ..., b_{k} must not have any neighbours in the tree other than adjacent vertices of corresponding paths. After that, one of the paths may be merged into the other, that is, the vertices b_1, ..., b_{k} can be effectively erased: [Image] Help Vanya determine if it possible to make the tree into a path via a sequence of described operations, and if the answer is positive, also determine the shortest length of such path. -----Input----- The first line of input contains the number of vertices n (2 ≤ n ≤ 2·10^5). Next n - 1 lines describe edges of the tree. Each of these lines contains two space-separated integers u and v (1 ≤ u, v ≤ n, u ≠ v) — indices of endpoints of the corresponding edge. It is guaranteed that the given graph is a tree. -----Output----- If it is impossible to obtain a path, print -1. Otherwise, print the minimum number of edges in a possible path. -----Examples----- Input 6 1 2 2 3 2 4 4 5 1 6 Output 3 Input 7 1 2 1 3 3 4 1 5 5 6 6 7 Output -1 -----Note----- In the first sample case, a path of three edges is obtained after merging paths 2 - 1 - 6 and 2 - 4 - 5. It is impossible to perform any operation in the second sample case. For example, it is impossible to merge paths 1 - 3 - 4 and 1 - 5 - 6, since vertex 6 additionally has a neighbour 7 that is not present in the corresponding path.

import math,string,itertools,fractions,heapq,collections,re,array,bisect,sys,random,time sys.setrecursionlimit(10**7) inf = 10**20 mod = 10**9 + 7 def LI(): return list(map(int, input().split())) def II(): return int(input()) def LS(): return input().split() def S(): return input() def main(): n = II() d = collections.defaultdict(set) for _ in range(n-1): a,b = LI() d[a].add(b) d[b].add(a) memo = [-1] * (n+1) def path(t,s): ps = set() dt = list(d[t]) for k in dt: if memo[k] < 0: continue ps.add(memo[k]) if s == -1 and len(ps) == 2: memo[t] = sum(ps) + 2 return memo[t] if len(ps) > 1: return -t if len(ps) == 0: memo[t] = 0 return 0 memo[t] = list(ps)[0] + 1 return memo[t] def _path(tt,ss): f = [False] * (n+1) q = [(tt,ss)] tq = [] qi = 0 while len(q) > qi: t,s = q[qi] for k in d[t]: if k == s or memo[k] >= 0: continue q.append((k,t)) qi += 1 for t,s in q[::-1]: r = path(t,s) if r < 0: return r return memo[tt] t = _path(1,-1) if t < 0: t = _path(-t,-1) if t > 0: while t%2 == 0: t//=2 return t return -1 print(main())

train

APPS_structured

Catherine received an array of integers as a gift for March 8. Eventually she grew bored with it, and she started calculated various useless characteristics for it. She succeeded to do it for each one she came up with. But when she came up with another one — xor of all pairwise sums of elements in the array, she realized that she couldn't compute it for a very large array, thus she asked for your help. Can you do it? Formally, you need to compute $$ (a_1 + a_2) \oplus (a_1 + a_3) \oplus \ldots \oplus (a_1 + a_n) \\ \oplus (a_2 + a_3) \oplus \ldots \oplus (a_2 + a_n) \\ \ldots \\ \oplus (a_{n-1} + a_n) \\ $$ Here $x \oplus y$ is a bitwise XOR operation (i.e. $x$ ^ $y$ in many modern programming languages). You can read about it in Wikipedia: https://en.wikipedia.org/wiki/Exclusive_or#Bitwise_operation. -----Input----- The first line contains a single integer $n$ ($2 \leq n \leq 400\,000$) — the number of integers in the array. The second line contains integers $a_1, a_2, \ldots, a_n$ ($1 \leq a_i \leq 10^7$). -----Output----- Print a single integer — xor of all pairwise sums of integers in the given array. -----Examples----- Input 2 1 2 Output 3 Input 3 1 2 3 Output 2 -----Note----- In the first sample case there is only one sum $1 + 2 = 3$. In the second sample case there are three sums: $1 + 2 = 3$, $1 + 3 = 4$, $2 + 3 = 5$. In binary they are represented as $011_2 \oplus 100_2 \oplus 101_2 = 010_2$, thus the answer is 2. $\oplus$ is the bitwise xor operation. To define $x \oplus y$, consider binary representations of integers $x$ and $y$. We put the $i$-th bit of the result to be 1 when exactly one of the $i$-th bits of $x$ and $y$ is 1. Otherwise, the $i$-th bit of the result is put to be 0. For example, $0101_2 \, \oplus \, 0011_2 = 0110_2$.

import sys input = sys.stdin.readline n = int(input()) a = list(map(int, input().split())) b = a ans = 0 for k in range(29): a0 = [] a1 = [] a0a = a0.append a1a = a1.append b0 = [] b1 = [] b0a = b0.append b1a = b1.append for i in a: if i&(1<<k): a1a(i) else: a0a(i) for i in b: if i&(1<<k): b1a(i) else: b0a(i) a = a0+a1 b = b0+b1 mask = (1<<(k+1))-1 aa = [i&mask for i in a] bb = [i&mask for i in b] res = 0 p1 = 1<<k p2 = mask+1 p3 = p1+p2 j1 = j2 = j3 = 0 for jj, ai in enumerate(reversed(aa)): while j1 < n and ai+bb[j1] < p1: j1 += 1 while j2 < n and ai+bb[j2] < p2: j2 += 1 while j3 < n and ai+bb[j3] < p3: j3 += 1 res += max(n, n - jj) - max(j3, n - jj) res += max(j2, n - jj) - max(j1, n - jj) ans |= (res & 1) << k print(ans)

train

APPS_structured

Prof. Sergio Marquina is a mathematics teacher at the University of Spain. Whenever he comes across any good question(with complexity k), he gives that question to students within roll number range i and j. At the start of the semester he assigns a score of 10 to every student in his class if a student submits a question of complexity k, his score gets multiplied by k. This month he gave M questions and he is wondering what will be mean of maximum scores of all the students. He is busy planning a tour of the Bank of Spain for his students, can you help him? -----Input:----- - First-line will contain $T$, the number of test cases. Then the test cases follow. - Each test case contains the first line of input, two integers N, M i.e. Number of students in the class and number of questions given in this month. - Next M lines contain 3 integers -i,j,k i.e. starting roll number, end roll number, and complexity of the question -----Output:----- - For each test case, output in a single line answer - floor value of Mean of the maximum possible score for all students. -----Constraints----- - $1 \leq T \leq 100$ - $1 \leq N, M \leq 105$ - $1 \leq i \leq j \leq N$ - $1 \leq k \leq 100$ -----Sample Input:----- 1 5 3 1 3 5 2 5 2 3 4 7 -----Sample Output:----- 202 -----EXPLANATION:----- Initial score of students will be : [10,10,10,10,10] after solving question 1 scores will be: [50,50,50,10,10] after solving question 2 scores will be: [50,100,100,20,20] after solving question 1 scores will be: [50,100,700,140,20] Hence after all questions mean of maximum scores will (50+100+700+140+20)/5=202

# cook your dish here t=int(input()) for _ in range(t): n,m=map(int,input().split()) a=list() for _ in range(n): a.append(10) for _ in range(m): i,j,k=map(int,input().split()) for z in range(i-1,j): a[z]=a[z]*k print(sum(a)//n)

train

APPS_structured

Chef has a pepperoni pizza in the shape of a $N \times N$ grid; both its rows and columns are numbered $1$ through $N$. Some cells of this grid have pepperoni on them, while some do not. Chef wants to cut the pizza vertically in half and give the two halves to two of his friends. Formally, one friend should get everything in the columns $1$ through $N/2$ and the other friend should get everything in the columns $N/2+1$ through $N$. Before doing that, if Chef wants to, he may choose one row of the grid and reverse it, i.e. swap the contents of the cells in the $i$-th and $N+1-i$-th column in this row for each $i$ ($1 \le i \le N/2$). After the pizza is cut, let's denote the number of cells containing pepperonis in one half by $p_1$ and their number in the other half by $p_2$. Chef wants to minimise their absolute difference. What is the minimum value of $|p_1-p_2|$? -----Input----- - The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows. - The first line of each test case contains a single integer $N$. - $N$ lines follow. For each $i$ ($1 \le i \le N$), the $i$-th of these lines contains a string with length $N$ describing the $i$-th row of the grid; this string contains only characters '1' (denoting a cell with pepperonis) and '0' (denoting a cell without pepperonis). -----Output----- For each test case, print a single line containing one integer — the minimum absolute difference between the number of cells with pepperonis in the half-pizzas given to Chef's friends. -----Constraints----- - $1 \le T \le 1,000$ - $2 \le N \le 1,000$ - $N$ is even - the sum of $N \cdot N$ over all test cases does not exceed $2 \cdot 10^6$ -----Example Input----- 2 6 100000 100000 100000 100000 010010 001100 4 0011 1100 1110 0001 -----Example Output----- 2 0 -----Explanation----- Example case 1: Initially, $|p_1-p_2| = 4$, but if Chef reverses any one of the first four rows from "100000" to "000001", $|p_1-p_2|$ becomes $2$. Example case 2: Initially, $|p_1-p_2| = 0$. We cannot make that smaller by reversing any row.

for t in range(int(input())): n=int(input()) p1=0 p2=0 ans=500 diff=[] for i in range(n): a=input() x=0 y=0 for j in range(n//2): if a[j]=='1': p1+=1 x+=1 for j in range(n//2,n): if a[j]=='1': p2+=1 y+=1 diff.append(2*(y-x)) for k in range(n): ans=min(ans,abs(p1-p2+diff[k])) print(min(ans,abs(p1-p2)))

train

APPS_structured

Chef's daily routine is very simple. He starts his day with cooking food, then he eats the food and finally proceeds for sleeping thus ending his day. Chef carries a robot as his personal assistant whose job is to log the activities of Chef at various instants during the day. Today it recorded activities that Chef was doing at N different instants. These instances are recorded in chronological order (in increasing order of time). This log is provided to you in form of a string s of length N, consisting of characters 'C', 'E' and 'S'. If s[i] = 'C', then it means that at the i-th instant Chef was cooking, 'E' denoting he was eating and 'S' means he was sleeping. You have to tell whether the record log made by the robot could possibly be correct or not. -----Input----- The first line of the input contains an integer T denoting the number of test cases. The description of T test cases follows. The only line of each test case contains string s. -----Output----- For each test case, output a single line containing "yes" or "no" (without quotes) accordingly. -----Constraints----- - 1 ≤ T ≤ 20 - 1 ≤ N ≤ 105 -----Subtasks----- - Subtask #1 (40 points) : 1 ≤ N ≤ 100 - Subtask #2 (60 points) : original constraints -----Example----- Input: 5 CES CS CCC SC ECCC Output: yes yes yes no no -----Explanation----- Example case 1. "CES" can correspond to a possible record of activities of Chef. He starts the day with cooking, then eating and then sleeping. Example case 2. "CS" can also correspond to a possible record of activities of Chef. He starts the day with cooking, then eating and then sleeping. Robot recorded his cooking and sleeping in order. He might not have recorded his eating activity. Example case 4. "SC" can not correspond to Chef's activities. Here it means that Chef slept first, then he cooked the food, which is impossible for Chef to do on some particular day.

# cook your dish here for _ in range(int(input())): s=input() n=len(s) ans="yes" st="CES" if n==1 : print(ans) continue elif n==2: for i in range (0,1): curr=s[i] if curr=='C' and (s[i+1]=='C' or s[i+1]=='E' or s[i+1]=='S'): continue elif curr=='E' and (s[i+1]=='E' or s[i+1]=='S'): continue elif curr=='S' and s[i+1]=='S': continue else: ans="no" break else: for i in range (0,n-2): curr=s[i] if curr=='C' and (s[i+1]=='C' or s[i+1]=='E' or s[i+1]=='S'): continue elif curr=='E' and (s[i+1]=='E' or s[i+1]=='S'): continue elif curr=='S' and s[i+1]=='S': continue else: ans="no" break print(ans)

train

APPS_structured

Let us define a function `f`such as: - (1) for k positive odd integer > 2 : - (2) for k positive even integer >= 2 : - (3) for k positive integer > 1 : where `|x|` is `abs(x)` and Bk the kth Bernoulli number. `f` is not defined for `0, 1, -1`. These values will not be tested. # Guidelines for Bernoulli numbers: https://en.wikipedia.org/wiki/Bernoulli_number http://mathworld.wolfram.com/BernoulliNumber.html https://www.codewars.com/kata/bernoulli-numbers-1 There is more than one way to calculate them. You can make Pascal triangle and then with the basic formula below generate all Bernoulli numbers. 1 + 2B1 = 0 ... gives ... B1 = - 1/2 1 + 3B1 + 3B2 = 0 ... gives ... B2 = 1/6 1 + 4B1 + 6B2 + 4B3 = 0 ... gives ... B3 = 0 1 + 5B1 + 10B2 + 10B3 + 5B4 = 0 ... gives ... B4 = - 1/30 ... and so on # Task Function `series(k, nb)` returns (1), (2) or (3) where `k` is the `k` parameter of `f` and `nb` the upper bound in the summation of (1). `nb` is of no use for (2) and (3) but for the sake of simplicity it will always appear in the tests even for cases (2) and (3) with a value of `0`. ``` Examples S(2, 0) = 1.644934066848224.... S(3, 100000) = 1.20205690310973.... S(4, 0) = 1.08232323371113..... S(-5, 0) = -0.003968253968.... S(-11, 0) = 0.02109279609279.... ``` # Notes - For Java, C#, C++: `k` should be such as `-27 <= k <= 20`; otherwise `-30 <= k <= 30` and be careful of 32-bit integer overflow. - Translators are welcome.

from math import factorial,pi from fractions import Fraction def comb(n,k): return factorial(n)//(factorial(n-k)*factorial(k)) def bernoulli(m): b=[1] for i in range(1,m+1): n=0 for k in range(0,i): n+=comb(i+1,k)*b[k] b.append(Fraction(-n,i+1)) return b b=bernoulli(31) def series(k, nb) : if k<0: k=-k return (b[k+1]*(-1)**k)/(k+1) elif k%2==1: return sum(1/(n**k) for n in range(1,nb+1)) else: return abs(b[k])*((2*pi)**k)/(2*factorial(k))

train

APPS_structured

Given two arrays of integers nums1 and nums2, return the number of triplets formed (type 1 and type 2) under the following rules: Type 1: Triplet (i, j, k) if nums1[i]2 == nums2[j] * nums2[k] where 0 <= i < nums1.length and 0 <= j < k < nums2.length. Type 2: Triplet (i, j, k) if nums2[i]2 == nums1[j] * nums1[k] where 0 <= i < nums2.length and 0 <= j < k < nums1.length. Example 1: Input: nums1 = [7,4], nums2 = [5,2,8,9] Output: 1 Explanation: Type 1: (1,1,2), nums1[1]^2 = nums2[1] * nums2[2]. (4^2 = 2 * 8). Example 2: Input: nums1 = [1,1], nums2 = [1,1,1] Output: 9 Explanation: All Triplets are valid, because 1^2 = 1 * 1. Type 1: (0,0,1), (0,0,2), (0,1,2), (1,0,1), (1,0,2), (1,1,2). nums1[i]^2 = nums2[j] * nums2[k]. Type 2: (0,0,1), (1,0,1), (2,0,1). nums2[i]^2 = nums1[j] * nums1[k]. Example 3: Input: nums1 = [7,7,8,3], nums2 = [1,2,9,7] Output: 2 Explanation: There are 2 valid triplets. Type 1: (3,0,2). nums1[3]^2 = nums2[0] * nums2[2]. Type 2: (3,0,1). nums2[3]^2 = nums1[0] * nums1[1]. Example 4: Input: nums1 = [4,7,9,11,23], nums2 = [3,5,1024,12,18] Output: 0 Explanation: There are no valid triplets. Constraints: 1 <= nums1.length, nums2.length <= 1000 1 <= nums1[i], nums2[i] <= 10^5

class Solution: def numTriplets(self, nums1: List[int], nums2: List[int]) -> int: table1 = {} table2 = {} res = 0 for n in nums1: square = n * n table = {} for j, m in enumerate(nums2): if square % m == 0: remainder = square // m if remainder in table: # print(square, m, remainder, table) res += table[remainder] if m not in table: table[m] = 0 table[m] += 1 for n in nums2: square = n * n table = {} for j, m in enumerate(nums1): if square % m == 0: remainder = square // m if remainder in table: # print(square, m, remainder, table) res += table[remainder] if m not in table: table[m] = 0 table[m] += 1 return res

train

APPS_structured

Cheesy Cheeseman just got a new monitor! He is happy with it, but he just discovered that his old desktop wallpaper no longer fits. He wants to find a new wallpaper, but does not know which size wallpaper he should be looking for, and alas, he just threw out the new monitor's box. Luckily he remembers the width and the aspect ratio of the monitor from when Bob Mortimer sold it to him. Can you help Cheesy out? # The Challenge Given an integer `width` and a string `ratio` written as `WIDTH:HEIGHT`, output the screen dimensions as a string written as `WIDTHxHEIGHT`.

from fractions import Fraction def find_screen_height(width, ratio): ratio = ratio.replace(":","/") ratio = float(sum(Fraction(s) for s in ratio.split())) return "{}x{}".format(width, int(width/ratio))

train

APPS_structured

Let's denote as $\text{popcount}(x)$ the number of bits set ('1' bits) in the binary representation of the non-negative integer x. You are given multiple queries consisting of pairs of integers l and r. For each query, find the x, such that l ≤ x ≤ r, and $\text{popcount}(x)$ is maximum possible. If there are multiple such numbers find the smallest of them. -----Input----- The first line contains integer n — the number of queries (1 ≤ n ≤ 10000). Each of the following n lines contain two integers l_{i}, r_{i} — the arguments for the corresponding query (0 ≤ l_{i} ≤ r_{i} ≤ 10^18). -----Output----- For each query print the answer in a separate line. -----Examples----- Input 3 1 2 2 4 1 10 Output 1 3 7 -----Note----- The binary representations of numbers from 1 to 10 are listed below: 1_10 = 1_2 2_10 = 10_2 3_10 = 11_2 4_10 = 100_2 5_10 = 101_2 6_10 = 110_2 7_10 = 111_2 8_10 = 1000_2 9_10 = 1001_2 10_10 = 1010_2

q=int(input()) for i in range(q): x,y=list(map(int,input().split())) diff=y-x x=bin(x)[2:] y=bin(y)[2:] x='0'*(len(y)-len(x))+x newString='' for j in range(len(x)): if x[len(x)-j-1]=='0': if diff>=2**j: newString+='1' diff-=2**j else: newString+='0' else: newString+='1' newString=newString[::-1] tot=0 ns=len(newString) for i in range(ns): tot+=int(newString[ns-i-1])*(2**i) print(tot)

train

APPS_structured

An expression is formed by taking the digits 1 to 9 in numerical order and then inserting into each gap between the numbers either a plus sign or a minus sign or neither. Your task is to write a method which takes one parameter and returns the **smallest possible number** of plus and minus signs necessary to form such an expression which equals the input. **Note:** All digits from 1-9 must be used exactly once. If there is no possible expression that evaluates to the input, then return `null/nil/None`. ~~~if:haskell `eval :: String -> Int` is available in `Preloaded` for your convenience. ~~~ There are 50 random tests with upper bound of the input = 1000. ## Examples When the input is 100, you need to return `3`, since that is the minimum number of signs required, because: 123 - 45 - 67 + 89 = 100 (3 operators in total). More examples: ``` 11 --> 5 # 1 + 2 + 34 + 56 + 7 - 89 = 11 100 --> 3 # 123 - 45 - 67 + 89 = 100 766 --> 4 # 1 - 2 + 34 - 56 + 789 = 766 160 --> - # no solution possible ``` Inspired by a [puzzle on BBC Radio 4](https://www.bbc.co.uk/programmes/p057wxwl) (which is unfortunately not available anymore)

from itertools import product, zip_longest def operator_insertor(n): inserts = [] for ops in product(('+', '-', ''), repeat=8): expression = ''.join(map(''.join, zip_longest('123456789', ops, fillvalue=''))) if eval(expression) == n: inserts.append(len(expression) - 9) return min(inserts, default=None)

train

APPS_structured

# Description: Replace the pair of exclamation marks and question marks to spaces(from the left to the right). A pair of exclamation marks and question marks must has the same number of "!" and "?". That is: "!" and "?" is a pair; "!!" and "??" is a pair; "!!!" and "???" is a pair; and so on.. # Examples ``` replace("!!") === "!!" replace("!??") === "!??" replace("!?") === " " replace("!!??") === " " replace("!!!????") === "!!!????" replace("!??!!") === "! " replace("!????!!!?") === " ????!!! " replace("!?!!??!!!?") === " !!!?" ```

from itertools import groupby def replace(s): queue, rle = {}, [[i, k, len(list(g))] for i, (k, g) in enumerate(groupby(s))] for i, k, l in reversed(rle): if l not in queue: queue[l] = {} queue[l].setdefault(k, []).append(i) for l in queue: while sum(map(bool, queue[l].values())) > 1: for c in queue[l]: rle[queue[l][c].pop()][1] = ' ' return ''.join(k * l for i, k, l in rle)

train

APPS_structured

# Task When a candle finishes burning it leaves a leftover. makeNew leftovers can be combined to make a new candle, which, when burning down, will in turn leave another leftover. You have candlesNumber candles in your possession. What's the total number of candles you can burn, assuming that you create new candles as soon as you have enough leftovers? # Example For candlesNumber = 5 and makeNew = 2, the output should be `9`. Here is what you can do to burn 9 candles: ``` burn 5 candles, obtain 5 leftovers; create 2 more candles, using 4 leftovers (1 leftover remains); burn 2 candles, end up with 3 leftovers; create another candle using 2 leftovers (1 leftover remains); burn the created candle, which gives another leftover (2 leftovers in total); create a candle from the remaining leftovers; burn the last candle. Thus, you can burn 5 + 2 + 1 + 1 = 9 candles, which is the answer. ``` # Input/Output - `[input]` integer `candlesNumber` The number of candles you have in your possession. Constraints: 1 ≤ candlesNumber ≤ 50. - `[input]` integer `makeNew` The number of leftovers that you can use up to create a new candle. Constraints: 2 ≤ makeNew ≤ 5. - `[output]` an integer

def candles(m, n): burn = leftover = 0 while m: burn += m m, leftover = divmod(leftover + m, n) return burn

train

APPS_structured

A Little Elephant from the Zoo of Lviv likes lucky strings, i.e., the strings that consist only of the lucky digits 4 and 7. The Little Elephant calls some string T of the length M balanced if there exists at least one integer X (1 ≤ X ≤ M) such that the number of digits 4 in the substring T[1, X - 1] is equal to the number of digits 7 in the substring T[X, M]. For example, the string S = 7477447 is balanced since S[1, 4] = 7477 has 1 digit 4 and S[5, 7] = 447 has 1 digit 7. On the other hand, one can verify that the string S = 7 is not balanced. The Little Elephant has the string S of the length N. He wants to know the number of such pairs of integers (L; R) that 1 ≤ L ≤ R ≤ N and the substring S[L, R] is balanced. Help him to find this number. Notes. Let S be some lucky string. Then - |S| denotes the length of the string S; - S[i] (1 ≤ i ≤ |S|) denotes the ith character of S (the numeration of characters starts from 1); - S[L, R] (1 ≤ L ≤ R ≤ |S|) denotes the string with the following sequence of characters: S[L], S[L + 1], ..., S[R], and is called a substring of S. For L > R we mean by S[L, R] an empty string. -----Input----- The first line of the input file contains a single integer T, the number of test cases. Each of the following T lines contains one string, the string S for the corresponding test case. The input file does not contain any whitespaces. -----Output----- For each test case output a single line containing the answer for this test case. -----Constraints----- 1 ≤ T ≤ 10 1 ≤ |S| ≤ 100000 S consists only of the lucky digits 4 and 7. -----Example----- Input: 4 47 74 477 4747477 Output: 2 2 3 23 -----Explanation----- In the first test case balance substrings are S[1, 1] = 4 and S[1, 2] = 47. In the second test case balance substrings are S[2, 2] = 4 and S[1, 2] = 74. Unfortunately, we can't provide you with the explanations of the third and the fourth test cases. You should figure it out by yourself. Please, don't ask about this in comments.

tcase=int(eval(input())) i=0 while(tcase): tcase-=1 a=str(input()) j=0 i=0 rem=0 length=len(a) ans=(length*(length+1))/2 #print ans, while(i<length): if(a[i]=='7'): rem+=(i-j+1) #print i,j, else: j=i+1 i+=1 ans-= rem; print(ans);

train

APPS_structured

Write a class StockSpanner which collects daily price quotes for some stock, and returns the span of that stock's price for the current day. The span of the stock's price today is defined as the maximum number of consecutive days (starting from today and going backwards) for which the price of the stock was less than or equal to today's price. For example, if the price of a stock over the next 7 days were [100, 80, 60, 70, 60, 75, 85], then the stock spans would be [1, 1, 1, 2, 1, 4, 6]. Example 1: Input: ["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]] Output: [null,1,1,1,2,1,4,6] Explanation: First, S = StockSpanner() is initialized. Then: S.next(100) is called and returns 1, S.next(80) is called and returns 1, S.next(60) is called and returns 1, S.next(70) is called and returns 2, S.next(60) is called and returns 1, S.next(75) is called and returns 4, S.next(85) is called and returns 6. Note that (for example) S.next(75) returned 4, because the last 4 prices (including today's price of 75) were less than or equal to today's price. Note: Calls to StockSpanner.next(int price) will have 1 <= price <= 10^5. There will be at most 10000 calls to StockSpanner.next per test case. There will be at most 150000 calls to StockSpanner.next across all test cases. The total time limit for this problem has been reduced by 75% for C++, and 50% for all other languages.

from math import floor from math import ceil from math import sqrt from collections import deque import numpy from _collections import deque #from _ast import Num # LC doesn't like this from heapq import * from typing import List import random MOD = int(1e9 + 7) BASE = 256 class StockSpanner: def __init__(self): self.s = [] self.i = 0 def next(self, price: int) -> int: s = self.s i = self.i while len(s) and s[-1][0] <= price: s.pop() ans = i + 1 if len(s): ans = i - s[-1][1] s.append((price, i)) self.i += 1 return ans # Your StockSpanner object will be instantiated and called as such: # obj = StockSpanner() # param_1 = obj.next(price) \"\"\" s = StockSpanner() print(s.next(100)) print(s.next(80)) print(s.next(60)) print(s.next(70)) print(s.next(60)) print(s.next(75)) print(s.next(85)) \"\"\"

train

APPS_structured

# Task Given an array of roots of a polynomial equation, you should reconstruct this equation. ___ ## Output details: * If the power equals `1`, omit it: `x = 0` instead of `x^1 = 0` * If the power equals `0`, omit the `x`: `x - 2 = 0` instead of `x - 2x^0 = 0` * There should be no 2 signs in a row: `x - 1 = 0` instead of `x + -1 = 0` * If the coefficient equals `0`, skip it: `x^2 - 1 = 0` instead of `x^2 + 0x - 1 = 0` * Repeating roots should not be filtered out: `x^2 - 4x + 4 = 0` instead of `x - 2 = 0` * The coefficient before `q^n` is always `1`: `x^n + ... = 0` instead of `Ax^n + ... = 0` ___ ## Example: ``` polynomialize([0]) => "x = 0" polynomialize([1]) => "x - 1 = 0" polynomialize([1, -1]) => "x^2 - 1 = 0" polynomialize([0, 2, 3]) => "x^3 - 5x^2 + 6x = 0" ``` ___ ## Tests: ```python Main suite: Edge cases: (Reference - 4000 ms) (Reference - 30 ms) N of roots | N of tests N of roots | N of tests ----------------------- ----------------------- 1-10 | 100 20-40 | 125 700-750 | 25 2-20 | 125 ```

import re def polynomialize(roots): def deploy(roots): r = -roots[0] if len(roots) == 1: return [r, 1] sub = deploy(roots[1:]) + [0] return [c*r + sub[i-1] for i,c in enumerate(sub)] coefs = deploy(roots) poly = ' + '.join(["{}x^{}".format(c,i) for i,c in enumerate(coefs) if c][::-1]) poly = re.sub(r'x\^0|\^1\b|\b1(?=x)(?!x\^0)', '', poly).replace("+ -", "- ") + ' = 0' return poly

train

APPS_structured

Polycarpus is a system administrator. There are two servers under his strict guidance — a and b. To stay informed about the servers' performance, Polycarpus executes commands "ping a" and "ping b". Each ping command sends exactly ten packets to the server specified in the argument of the command. Executing a program results in two integers x and y (x + y = 10; x, y ≥ 0). These numbers mean that x packets successfully reached the corresponding server through the network and y packets were lost. Today Polycarpus has performed overall n ping commands during his workday. Now for each server Polycarpus wants to know whether the server is "alive" or not. Polycarpus thinks that the server is "alive", if at least half of the packets that we send to this server reached it successfully along the network. Help Polycarpus, determine for each server, whether it is "alive" or not by the given commands and their results. -----Input----- The first line contains a single integer n (2 ≤ n ≤ 1000) — the number of commands Polycarpus has fulfilled. Each of the following n lines contains three integers — the description of the commands. The i-th of these lines contains three space-separated integers t_{i}, x_{i}, y_{i} (1 ≤ t_{i} ≤ 2; x_{i}, y_{i} ≥ 0; x_{i} + y_{i} = 10). If t_{i} = 1, then the i-th command is "ping a", otherwise the i-th command is "ping b". Numbers x_{i}, y_{i} represent the result of executing this command, that is, x_{i} packets reached the corresponding server successfully and y_{i} packets were lost. It is guaranteed that the input has at least one "ping a" command and at least one "ping b" command. -----Output----- In the first line print string "LIVE" (without the quotes) if server a is "alive", otherwise print "DEAD" (without the quotes). In the second line print the state of server b in the similar format. -----Examples----- Input 2 1 5 5 2 6 4 Output LIVE LIVE Input 3 1 0 10 2 0 10 1 10 0 Output LIVE DEAD -----Note----- Consider the first test case. There 10 packets were sent to server a, 5 of them reached it. Therefore, at least half of all packets sent to this server successfully reached it through the network. Overall there were 10 packets sent to server b, 6 of them reached it. Therefore, at least half of all packets sent to this server successfully reached it through the network. Consider the second test case. There were overall 20 packages sent to server a, 10 of them reached it. Therefore, at least half of all packets sent to this server successfully reached it through the network. Overall 10 packets were sent to server b, 0 of them reached it. Therefore, less than half of all packets sent to this server successfully reached it through the network.

n = int(input()) a = [[0,0],[0,0]] for i in range(n): t,x,y = map(int, input().split()) a[t-1][0] += x a[t-1][1] += 5 if a[0][0] >= a[0][1]: print('LIVE') else: print('DEAD') if a[1][0] >= a[1][1]: print('LIVE') else: print('DEAD')

train

APPS_structured

There is Chef and Chef’s Crush who are playing a game of numbers. Chef’s crush has a number $A$ and Chef has a number $B$. Now, Chef wants Chef’s crush to win the game always, since she is his crush. The game ends when the greatest value of A^B is reached after performing some number of operations (possibly zero), Where ^ is Bitwise XOR. Before performing any operation you have to ensure that both $A$ and $B$ have the same number of bits without any change in the values. It is not guaranteed that $A$ and $B$ should have same number of bits in the input. For example, if $A$ is $2$ and $B$ is $15$, then the binary representation of both the numbers will have to be $0010$ and $1111$ respectively, before performing any operation. The operation is defined as : - Right circular shift of the bits of only $B$ from MSB$_B$ to LSB$_B$ i.e. if we consider $B_1 B_2 B_3 B_4$ as binary number, then after one circular right shift, it would be $B_4 B_1 B_2 B_3$ They both are busy with themselves, can you find the number of operations to end the game? -----Input :----- - The first line of input contains $T$, (number of test cases) - Then each of the next $T$ lines contain : two integers $A$ and $B$ respectively. -----Output :----- For each test case print two space-separated integers, The number of operations to end the game and value of A^B when the game ends. -----Constraints :----- - $1 \leq T \leq100$ - $1\leq A,B \leq 10^{18}$ -----Subtasks :----- - 30 Points: $1\leq A,B \leq 10^5$ - 70 Points: Original Constraints -----Sample Input :----- 1 4 5 -----Sample Output :----- 2 7 -----Explanation :----- Binary representation of $4$ is $100$ and binary representation $5$ is $101$. - After operation $1$ : $B$ $=$ $110$, so A^B $=$ $2$ - After operation $2$ : $B$ $=$ $011$, so A^B $=$ $7$ So, the value of A^B will be $7$. Which is the greatest possible value for A^B and the number of operations are $2$.

for _ in range(int(input())): a,b=list(map(int,input().split())) ab=bin(a)[2:] bb=bin(b)[2:] n=abs(len(bb)-len(ab)) if n>0: if len(bb)>len(ab): ab = "0"*n + ab else: bb = "0"*n + bb m=0 count=0 for i in range(len(bb)): l=int(ab,2)^int(bb,2) if l>m: m=l count=i bb =bb[-1] + bb bb=bb[:-1] print(count,m)

train

APPS_structured

Chef's company wants to make ATM PINs for its users, so that they could use the PINs for withdrawing their hard-earned money. One of these users is Reziba, who lives in an area where a lot of robberies take place when people try to withdraw their money. Chef plans to include a safety feature in the PINs: if someone inputs the reverse of their own PIN in an ATM machine, the Crime Investigation Department (CID) are immediately informed and stop the robbery. However, even though this was implemented by Chef, some people could still continue to get robbed. The reason is that CID is only informed if the reverse of a PIN is different from that PIN (so that there wouldn't be false reports of robberies). You know that a PIN consists of $N$ decimal digits. Find the probability that Reziba could get robbed. Specifically, it can be proven that this probability can be written as a fraction $P/Q$, where $P \ge 0$ and $Q > 0$ are coprime integers; you should compute $P$ and $Q$. -----Input----- - The first line of the input contains a single integer $T$ denoting the number of test cases. The description of $T$ test cases follows. - The first and only line of each test case contains a single integer $N$ denoting the length of each PIN. -----Output----- For each test case, print a single line containing two space-separated integers — the numerator $P$ and denominator $Q$ of the probability. -----Constraints----- - $1 \le T \le 100$ - $1 \le N \le 10^5$ -----Subtasks----- Subtask #1 (10 points): $N \le 18$ Subtask #2 (20 points): $N \le 36$ Subtask #3 (70 points): original constraints -----Example Input----- 1 1 -----Example Output----- 1 1 -----Explanation----- Example case 1: A PIN containing only one number would fail to inform the CID, since when it's input in reverse, the ATM detects the same PIN as the correct one. Therefore, Reziba can always get robbed — the probability is $1 = 1/1$.

# cook your dish here for _ in range(int(input())): n=int(input()) q="1"+"0"*(n//2) print(1,q)

train

APPS_structured

The chef is trying to decode some pattern problems, Chef wants your help to code it. Chef has one number K to form a new pattern. Help the chef to code this pattern problem. -----Input:----- - First-line will contain $T$, the number of test cases. Then the test cases follow. - Each test case contains a single line of input, one integer $K$. -----Output:----- For each test case, output as the pattern. -----Constraints----- - $1 \leq T \leq 100$ - $1 \leq K \leq 100$ -----Sample Input:----- 4 1 2 3 4 -----Sample Output:----- 1 1 01 11 001 1 01 11 001 101 011 111 0001 1001 1 01 11 001 101 011 111 0001 1001 0101 1101 0011 1011 0111 1111 00001 -----EXPLANATION:----- No need, else pattern can be decode easily.

t=int(input()) while(t): n=int(input()) cnt=1; for i in range(n): s="" for j in range(n): s=s+str(bin(cnt))[2:][: : -1]+" " cnt=cnt+1 print(s) t=t-1

train

APPS_structured

This is the easy version of the problem. The only difference between easy and hard versions is the constraint of $m$. You can make hacks only if both versions are solved. Chiori loves dolls and now she is going to decorate her bedroom![Image] As a doll collector, Chiori has got $n$ dolls. The $i$-th doll has a non-negative integer value $a_i$ ($a_i < 2^m$, $m$ is given). Chiori wants to pick some (maybe zero) dolls for the decoration, so there are $2^n$ different picking ways. Let $x$ be the bitwise-xor-sum of values of dolls Chiori picks (in case Chiori picks no dolls $x = 0$). The value of this picking way is equal to the number of $1$-bits in the binary representation of $x$. More formally, it is also equal to the number of indices $0 \leq i < m$, such that $\left\lfloor \frac{x}{2^i} \right\rfloor$ is odd. Tell her the number of picking ways with value $i$ for each integer $i$ from $0$ to $m$. Due to the answers can be very huge, print them by modulo $998\,244\,353$. -----Input----- The first line contains two integers $n$ and $m$ ($1 \le n \le 2 \cdot 10^5$, $0 \le m \le 35$) — the number of dolls and the maximum value of the picking way. The second line contains $n$ integers $a_1, a_2, \ldots, a_n$ ($0 \le a_i < 2^m$) — the values of dolls. -----Output----- Print $m+1$ integers $p_0, p_1, \ldots, p_m$ — $p_i$ is equal to the number of picking ways with value $i$ by modulo $998\,244\,353$. -----Examples----- Input 4 4 3 5 8 14 Output 2 2 6 6 0 Input 6 7 11 45 14 9 19 81 Output 1 2 11 20 15 10 5 0

MOD = 998244353 BOUND = 19 n, m = list(map(int, input().split())) l = list(map(int,input().split())) basis = [] for p in range(m-1,-1,-1): p2 = pow(2,p) nex = -1 for i in range(n): if l[i] >= p2: nex = l[i] break if nex != -1: basis.append(nex) for i in range(n): if l[i] >= p2: l[i] ^= nex extra = n - len(basis) def add(a, b): out = [0] * (max(len(a), len(b))) for i in range(len(a)): out[i] = a[i] for i in range(len(b)): out[i] += b[i] out[i] %= MOD return out def addSh(a, b): out = [0] * (max(len(a) + 1, len(b))) for i in range(len(a)): out[i + 1] = a[i] for i in range(len(b)): out[i] += b[i] out[i] %= MOD return out i = 0 curr = dict() curr[0] = [1] for p in range(m-1,-1,-1): p2 = pow(2,p) if i < len(basis) and basis[i] >= p2: currN = dict(curr) for v in curr: if v ^ basis[i] not in currN: currN[v ^ basis[i]] = [0] currN[v ^ basis[i]] = add(curr[v], currN[v ^ basis[i]]) curr = currN i += 1 currN = dict(curr) for v in curr: if v >= p2: if v ^ p2 not in currN: currN[v ^ p2] = [0] currN[v ^ p2] = addSh(curr[v], currN[v ^ p2]) del currN[v] curr = currN out = curr[0] while len(out) < m + 1: out.append(0) for i in range(m + 1): out[i] *= pow(2, extra, MOD) out[i] %= MOD print(' '.join(map(str,out)))

train

APPS_structured

# Convert number to reversed array of digits Given a random non-negative number, you have to return the digits of this number within an array in reverse order. ## Example: ``` 348597 => [7,9,5,8,4,3] ```

def digitize(n): lst = [int(i) for i in str(n)] #lst = lst.reverse() return lst[::-1]

train

APPS_structured

Given an integer array with all positive numbers and no duplicates, find the number of possible combinations that add up to a positive integer target. Example: nums = [1, 2, 3] target = 4 The possible combination ways are: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) Note that different sequences are counted as different combinations. Therefore the output is 7. Follow up: What if negative numbers are allowed in the given array? How does it change the problem? What limitation we need to add to the question to allow negative numbers? Credits:Special thanks to @pbrother for adding this problem and creating all test cases.

class Solution: # recursive, time limit exceeded def combinationSum4_1(self, nums, target): """ :type nums: List[int] :type target: int :rtype: int """ res = 0 if target == 0: return 1 for i in range(len(nums)): if target >= nums[i]: res += self.combinationSum4(nums, target - nums[i]) return res # top down using memory def combinationSum4_2(self, nums, target): """ :type nums: List[int] :type target: int :rtype: int """ dp = [-1] * (target + 1) dp[0] = 1 return self.helper(dp, nums, target) def helper(self, dp, nums, target): if dp[target] != -1: return dp[target] res = 0 for i in range(len(nums)): if target >= nums[i]: res += self.helper(dp, nums, target - nums[i]) dp[target] = res return res # bottom up def combinationSum4(self, nums, target): """ :type nums: List[int] :type target: int :rtype: int """ dp = [0] * (target + 1) dp[0] = 1 for i in range(target + 1): for num in sorted(nums): if i < num: break dp[i] += dp[i - num] return dp[-1]

train

APPS_structured

Given an array of ones and zeroes, convert the equivalent binary value to an integer. Eg: `[0, 0, 0, 1]` is treated as `0001` which is the binary representation of `1`. Examples: ``` Testing: [0, 0, 0, 1] ==> 1 Testing: [0, 0, 1, 0] ==> 2 Testing: [0, 1, 0, 1] ==> 5 Testing: [1, 0, 0, 1] ==> 9 Testing: [0, 0, 1, 0] ==> 2 Testing: [0, 1, 1, 0] ==> 6 Testing: [1, 1, 1, 1] ==> 15 Testing: [1, 0, 1, 1] ==> 11 ``` However, the arrays can have varying lengths, not just limited to `4`.

def binary_array_to_number(arr): return sum(digit * 2**i for i, digit in enumerate(reversed(arr)))

train

APPS_structured

Given an arbitrary ransom note string and another string containing letters from all the magazines, write a function that will return true if the ransom note can be constructed from the magazines ; otherwise, it will return false. Each letter in the magazine string can only be used once in your ransom note. Note: You may assume that both strings contain only lowercase letters. canConstruct("a", "b") -> false canConstruct("aa", "ab") -> false canConstruct("aa", "aab") -> true

class Solution: def canConstruct(self, ransomNote, magazine): """ :type ransomNote: str :type magazine: str :rtype: bool """ for i in set(ransomNote): if ransomNote.count(i) > magazine.count(i): return False return True

train

APPS_structured

What adds up =========== Given three arrays of integers your task is to create an algorithm that finds the numbers in the first two arrays whose sum is equal to any number in the third. The return value should be an array containing the values from the argument arrays that adds up. The sort order of the resulting array is not important. If no combination of numbers adds up return a empty array. ### Example A small example: Given the three input arrays `a1 = [1, 2]; a2 = [4,3]; a3 = [6,5,8]`, we need to find the number pairs from `a1` and `a2` that sum up to a number in `a3` and return those three numbers in an array. In this example, the result from the function would be `[[1, 4, 5] , [2, 4, 6], [2, 3, 5]]`. ``` Given three arrays a1 a2 a3 1 4 6 (a1 a2 a3) (a1 a2 a3) (a1 a2 a3) 2 3 5 => [[1, 4, 5] , [2, 4, 6], [2, 3, 5]] 8 each value in the result array contains one part from each of the arguments. ``` ### Testing A function `compare_array` is given. This function takes two arrays and compares them invariant of sort order. ```python test.expect(compare_arrays(addsup([1,2], [3,1], [5,4]), [[1,3,4], [2,3,5]])) ``` ### Greater goal For extra honor try and make it as effective as possible. Discuss whats the most effective way of doing this. The fastest way i can do this is in *O(n^2)*. Can you do it quicker?

def addsup(a1, a2, a3): a3 = set(a3) return [[x1, x2, x1 + x2] for x1 in a1 for x2 in a2 if x1 + x2 in a3]

train

APPS_structured

Write a function that outputs the transpose of a matrix - a new matrix where the columns and rows of the original are swapped. For example, the transpose of: | 1 2 3 | | 4 5 6 | is | 1 4 | | 2 5 | | 3 6 | The input to your function will be an array of matrix rows. You can assume that each row has the same length, and that the height and width of the matrix are both positive.

import numpy as np def transpose(matrix): return np.transpose(matrix).tolist()

train

APPS_structured

Chef belongs to a very rich family which owns many gold mines. Today, he brought N gold coins and decided to form a triangle using these coins. Isn't it strange? Chef has a unusual way of forming a triangle using gold coins, which is described as follows: - He puts 1 coin in the 1st row. - then puts 2 coins in the 2nd row. - then puts 3 coins in the 3rd row. - and so on as shown in the given figure. Chef is interested in forming a triangle with maximum possible height using at most N coins. Can you tell him the maximum possible height of the triangle? -----Input----- The first line of input contains a single integer T denoting the number of test cases. The first and the only line of each test case contains an integer N denoting the number of gold coins Chef has. -----Output----- For each test case, output a single line containing an integer corresponding to the maximum possible height of the triangle that Chef can get. -----Constraints----- - 1 ≤ T ≤ 100 - 1 ≤ N ≤ 109 -----Subtasks----- - Subtask 1 (48 points) : 1 ≤ N ≤ 105 - Subtask 2 (52 points) : 1 ≤ N ≤ 109 -----Example----- Input3 3 5 7 Output2 2 3 -----Explanation----- - Test 1: Chef can't form a triangle with height > 2 as it requires atleast 6 gold coins. - Test 2: Chef can't form a triangle with height > 2 as it requires atleast 6 gold coins. - Test 3: Chef can't form a triangle with height > 3 as it requires atleast 10 gold coins.

t = int(input()) for x in range(t): n = int(input()) n *= 2 a = int(n ** 0.5) if a*(a+1) <= n: print(a) else: print(a-1)

train

APPS_structured

Given a positive integer N, return the number of positive integers less than or equal to N that have at least 1 repeated digit. Example 1: Input: 20 Output: 1 Explanation: The only positive number (<= 20) with at least 1 repeated digit is 11. Example 2: Input: 100 Output: 10 Explanation: The positive numbers (<= 100) with atleast 1 repeated digit are 11, 22, 33, 44, 55, 66, 77, 88, 99, and 100. Example 3: Input: 1000 Output: 262 Note: 1 <= N <= 10^9

class Solution: def numDupDigitsAtMostN(self, N: int) -> int: N = str(N) @lru_cache(None) def dfs(i, r, m): if i == len(N): return 1 ans = 0 limit = int(N[i]) if r else 9 for k in range(0,limit+1): if m & (1 << k) == 0: mask = m | (1 << k) if m or k > 0 else 0 if k < limit or not r: ans += dfs(i+1, False, mask) else: ans += dfs(i+1, True, mask) return ans return int(N) - dfs(0, True, 0) + 1

train

APPS_structured

Similar to the [previous kata](https://www.codewars.com/kata/string-subpattern-recognition-ii/), but this time you need to operate with shuffled strings to identify if they are composed repeating a subpattern Since there is no deterministic way to tell which pattern was really the original one among all the possible permutations of a fitting subpattern, return a subpattern with sorted characters, otherwise return the base string with sorted characters (you might consider this case as an edge case, with the subpattern being repeated only once and thus equalling the original input string). For example: ```python has_subpattern("a") == "a"; #no repeated pattern, just one character has_subpattern("aaaa") == "a" #just one character repeated has_subpattern("abcd") == "abcd" #base pattern equals the string itself, no repetitions has_subpattern("babababababababa") == "ab" #remember to return the base string sorted" has_subpattern("bbabbaaabbaaaabb") == "ab" #same as above, just shuffled ``` If you liked it, go for either the [previous kata](https://www.codewars.com/kata/string-subpattern-recognition-ii/) or the [next kata](https://www.codewars.com/kata/string-subpattern-recognition-iv/) of the series!

from collections import Counter from functools import reduce from math import gcd def has_subpattern(string): chars_frequency = Counter(string) greatercd = reduce(gcd, chars_frequency.values()) charslist = sorted(chars_frequency.items()) pattern = "" for char, frequency in charslist: pattern += char * (frequency // greatercd) return pattern

train

APPS_structured

Lets wish Horsbug98 on his birthday and jump right into the question. In Chefland, $6$ new mobile brands have appeared each providing a range of smartphones. For simplicity let the brands be represented by numbers $1$ to $6$. All phones are sold at the superstore. There are total $N$ smartphones. Let $P_i$ & $B_i$ be the price and the brand of the $i^{th}$ smartphone. The superstore knows all the price and brand details beforehand. Each customer has a preference for brands. The preference is a subset of the brands available (i.e $1$ to $6$). Also, the customer will buy the $K^{th}$ costliest phone among all the phones of his preference. You will be asked $Q$ queries. Each query consists of the preference of the customer and $K$. Find the price the customer has to pay for his preference. If no such phone is available, print $-1$ Note that for each query the total number of smartphones is always $N$ since, after each purchase, the phones are replaced instantly. -----Input:----- - First Line contains $N$ and $Q$ - Second-line contains $N$ integers $P_1,P_2,...,P_N$ (Price) - Third line contains $N$ integers $B_1,B_2,...,B_N$ (Brand) - Each of the next Q lines contains a query, the query is describes below - First line of each quey contains $b$ and $K$ where $b$ is the size of the preference subset. - Second line of each query contains $b$ integers, describing the preference subset. -----Output:----- For each query, print the price to be paid. -----Constraints----- - $1 \leq N, Q, P_i \leq 10^5$ - $1 \leq B_i, b \leq 6$ - $1 \leq K \leq N$ -----Sample Input:----- 4 2 4 5 6 7 1 2 3 4 3 3 1 2 3 3 4 4 5 6 -----Sample Output:----- 4 -1 -----Explaination----- Query 1: The preference subset is {1, 2, 3}, The prices of phones available of these brands are {4, 5, 6}. The third costliest phone is 4. Query 2: The preference subset is {4, 5, 6}, The prices of phones available of these brands are {7}. Fouth costliest phone is required, which is not available. Hence, answer is $-1$.

import sys from collections import defaultdict from copy import copy R = lambda t = int: t(eval(input())) RL = lambda t = int: [t(x) for x in input().split()] RLL = lambda n, t = int: [RL(t) for _ in range(n)] def solve(): N, Q = RL() P = RL() B = RL() phones = sorted(zip(P, B)) S = defaultdict(lambda : []) for p, b in phones: for i in range(2**7): if (i>>b) & 1: S[i] += [p] B = set(B) I = [0] * len(B) for _ in range(Q): b, K = RL() s = RL() x = 0 for b in s: x += 1<<b if len(S[x]) < K: print(-1) else: print(S[x][-K]) T = 1#R() for t in range(1, T + 1): solve()

train

APPS_structured

Fibonacci numbers are generated by setting F0 = 0, F1 = 1, and then using the formula: # Fn = Fn-1 + Fn-2 Your task is to efficiently calculate the **n**th element in the Fibonacci sequence and then count the occurrence of each digit in the number. Return a list of integer pairs sorted in **descending** order. 10 ≤ n ≤ 100000 ## Examples ``` f(10) = 55 # returns [(2, 5)], as there are two occurances of digit 5 f(10000) # returns: [(254, 3), (228, 2), (217, 6), (217, 0), (202, 5), (199, 1), (198, 7), (197, 8), (194, 4), (184, 9)] ``` If two integers have the same count, sort them in descending order. Your algorithm must be efficient. ~~~if:javascript Solving this Kata in Javascript requires the use of the bignumber.js library. I have included starter code to assist you with using the library. Thanks to `kazk` for assisting with the translation. ~~~

def fib_digits(n): numCount = [[0,0], [0,1], [0,2], [0,3], [0,4], [0,5], [0,6], [0,7], [0,8], [0,9]] # 2d array of the amounts of each number a,b = 1,1 for i in range(n-1): # calculate the fibonacci number of the entered digit a,b = b,a+b fib_list = list(str(a)) # create a list of the numbers (in string form), one number per item i = 0 while i < len(fib_list): numCount[int(fib_list[i])][0] += 1 # if number is x, the number of x's is incremented i+=1 i = 0 while i < len(numCount): numCount[i] = tuple(numCount[i]) # convert each list item to tuple if numCount[i][0] == 0: numCount.pop(i) # if there aren't any of a specific number, remove it else: i+=1 return sorted(numCount, key=lambda x: (x[0], x[1]), reverse=True) # return the sorted list

train

APPS_structured

# Introduction The Condi (Consecutive Digraphs) cipher was introduced by G4EGG (Wilfred Higginson) in 2011. The cipher preserves word divisions, and is simple to describe and encode, but it's surprisingly difficult to crack. # Encoding Algorithm The encoding steps are: - Start with an `initial key`, e.g. `cryptogram` - Form a `key`, remove the key duplicated letters except for the first occurrence - Append to it, in alphabetical order all letters which do not occur in the `key`. The example produces: `cryptogambdefhijklnqsuvwxz` - Number the `key alphabet` starting with 1. ```python 1 2 3 4 5 6 7 8 9 10 11 12 13 c r y p t o g a m b d e f 14 15 16 17 18 19 20 21 22 23 24 25 26 h i j k l n q s u v w x z ``` - One of the inputs to encoding algorithm is an `initial shift`, say `10` - Encode the first letter of your `message` by moving 10 places to the right from the letter's position in the key alphabet. If the first letter were say `o` then the letter 10 places to the right in the `key alphabet` is `j`, so `o` would be encoded as `j`. If you move past the end of the key alphabet you wrap back to the beginning. For example if the first letter were `s` then counting 10 places would bring you around to `t`. - Use the position of the previous plaintext letter as the number of places to move to encode the next plaintext number. If you have just encoded an `o` (position 6) , and you now want to encode say `n`, then you move 6 places to the right from `n` which brings you to `x`. - Keep repeating the previous step until all letters are encoded. Decoding is the reverse of encoding - you move to the left instead of to the right. # Task Create two functions - `encode`/`Encode` and `decode`/`Decode` which implement Condi cipher encoding and decoding. # Inputs - `message` - a string to encode/decode - `key` - a key consists of only lower case letters - `initShift` - a non-negative integer representing the initial shift # Notes - Don't forget to remove the duplicated letters from the `key` except for the first occurrence - Characters which do not exist in the `key alphabet` should be coppied to the output string exactly like they appear in the `message` string - Check the test cases for samples

def encode(message, key, shift): return cipher(message, key, shift, 1) def decode(message, key, shift): return cipher(message, key, -shift, 0) def cipher(message, key, shift, mode): key = tuple(dict.fromkeys(key.lower() + 'abcdefghijklmnopqrstuvwxyz')) res = '' for char in message: if char in key: i = key.index(char) char = key[(i + shift) % 26] shift = i + 1 if mode else -key.index(char) - 1 res += char return res

train

APPS_structured

Complete the solution so that the function will break up camel casing, using a space between words. ### Example ``` solution("camelCasing") == "camel Casing" ```

def solution(s): newStr = "" for letter in s: if letter.isupper(): newStr += " " newStr += letter return newStr

train

APPS_structured

Mr. Khalkhoul, an amazing teacher, likes to answer questions sent by his students via e-mail, but he often doesn't have the time to answer all of them. In this kata you will help him by making a program that finds some of the answers. You are given a `question` which is a string containing the question and some `information` which is a list of strings representing potential answers. Your task is to find among `information` the UNIQUE string that has the highest number of words in common with `question`. We shall consider words to be separated by a single space. You can assume that: * all strings given contain at least one word and have no leading or trailing spaces, * words are composed with alphanumeric characters only You must also consider the case in which you get no matching words (again, ignoring the case): in such a case return `None/nil/null`. Mr. Khalkhoul is countin' on you :)

def answer(s, a): s = set(s.lower().split()) a = [(x, set(x.lower().split())) for x in a] r = max(a, key=lambda x: len(x[1] & s)) if r[1] & s: return r[0]

train

APPS_structured

Alice likes prime numbers. According to Alice, only those strings are nice whose sum of character values at a prime position is prime. She has a string $S$. Now, she has to count the number of nice strings which come before string $S$( including $S$) in the dictionary and are of the same length as $S$. Strings are zero-indexed from left to right. To find the character value she uses the mapping {'a': 0, 'b':1, 'c':2 ……. 'y': 24, 'z':25} . For example, for string $abcde$ Characters at prime positions are $'c'$ and $'d'$. c + d = 2 + 3 = 5. Since, 5 is a prime number, the string is $nice$. Since there could be many nice strings print the answer modulo $10^{9}+7$. -----Input:----- - First line will contain $T$, number of testcases. Then the testcases follow. - Each testcase contains of a single line of input, the string $S$. -----Output:----- For each testcase, output in a single line number of nice strings modulo $10^{9}+7$. -----Constraints----- - $1 \leq T \leq 10$ - $2 \leq |S| \leq 10^2$ String $S$ contains only lowercase letters. -----Sample Input:----- 1 abc -----Sample Output:----- 10

import sys from collections import defaultdict from copy import copy MOD = 10**9 + 7 R = lambda t = int: t(input()) RL = lambda t = int: [t(x) for x in input().split()] RLL = lambda n, t = int: [RL(t) for _ in range(n)] # primes up to n def primes(n): P = [] n = int(n) U = [1] * (n+1) p = 2 while p <= n: if U[p]: P += [p] x = p while x <= n: U[x] = 0 x += p p += 1 return P def solve(): S = R(str).strip() X = [ord(c)-ord('a') for c in S] P = primes(10000) L = defaultdict(lambda : 0) s = 0 for i in range(len(S)): p = i in P NL = defaultdict(lambda : 0) for a in range(26): for l in L: NL[l + a * p] += L[l] for a in range(X[i]): NL[s + a * p] += 1 s += X[i] * p L = NL L[s] += 1 r = 0 for p in P: r += L[p] print(r % MOD) T = R() for t in range(1, T + 1): solve()

train

APPS_structured

The number n is Evil if it has an even number of 1's in its binary representation. The first few Evil numbers: 3, 5, 6, 9, 10, 12, 15, 17, 18, 20 The number n is Odious if it has an odd number of 1's in its binary representation. The first few Odious numbers: 1, 2, 4, 7, 8, 11, 13, 14, 16, 19 You have to write a function that determine if a number is Evil of Odious, function should return "It's Evil!" in case of evil number and "It's Odious!" in case of odious number. good luck :)

def evil(n): return "It's " + ("Evil!" if bin(n).count("1")%2==0 else "Odious!")

train

APPS_structured

# Task **_Given_** an *array/list [] of n integers* , *find maximum triplet sum in the array* **_Without duplications_** . ___ # Notes : * **_Array/list_** size is *at least 3* . * **_Array/list_** numbers could be a *mixture of positives , negatives and zeros* . * **_Repetition_** of numbers in *the array/list could occur* , So **_(duplications are not included when summing)_**. ___ # Input >> Output Examples ## **_Explanation_**: * As the **_triplet_** that *maximize the sum* **_{6,8,3}_** in order , **_their sum is (17)_** * *Note* : **_duplications_** *are not included when summing* , **(i.e) the numbers added only once** . ___ ## **_Explanation_**: * As the **_triplet_** that *maximize the sum* **_{8, 6, 4}_** in order , **_their sum is (18)_** , * *Note* : **_duplications_** *are not included when summing* , **(i.e) the numbers added only once** . ___ ## **_Explanation_**: * As the **_triplet_** that *maximize the sum* **_{12 , 29 , 0}_** in order , **_their sum is (41)_** , * *Note* : **_duplications_** *are not included when summing* , **(i.e) the numbers added only once** . ___ # [Playing with Numbers Series](https://www.codewars.com/collections/playing-with-numbers) # [Playing With Lists/Arrays Series](https://www.codewars.com/collections/playing-with-lists-slash-arrays) # [For More Enjoyable Katas](http://www.codewars.com/users/MrZizoScream/authored) ___ ___ ___ ## ALL translations are welcomed ## Enjoy Learning !! # Zizou

def max_tri_sum(numbers): #your code here n = list(set(numbers)) n.sort(reverse=True) return sum(n[:3])

train

APPS_structured

The goal of this kata is to write a function that takes two inputs: a string and a character. The function will count the number of times that character appears in the string. The count is case insensitive. For example: ```python count_char("fizzbuzz","z") => 4 count_char("Fancy fifth fly aloof","f") => 5 ``` The character can be any alphanumeric character. Good luck.

def count_char(a,b): a=a.lower() b=b.lower() return a.count(b)

train

APPS_structured

Chef has decided to retire and settle near a peaceful beach. He had always been interested in literature & linguistics. Now when he has leisure time, he plans to read a lot of novels and understand structure of languages. Today he has decided to learn a difficult language called Smeagolese. Smeagolese is an exotic language whose alphabet is lowercase and uppercase roman letters. Also every word on this alphabet is a meaningful word in Smeagolese. Chef, we all know is a fierce learner - he has given himself a tough exercise. He has taken a word and wants to determine all possible anagrams of the word which mean something in Smeagolese. Can you help him ? -----Input----- Input begins with a single integer T, denoting the number of test cases. After that T lines follow each containing a single string S - the word chef has chosen. You can assume that 1 <= T <= 500 and 1 <= |S| <= 500. You can also assume that no character repeats more than 10 times in the string. -----Output----- Output one line per test case - the number of different words that are anagrams of the word that chef has chosen. As answer can get huge, print it modulo 10^9 + 7 -----Example----- Input: 4 ab aa aA AAbaz Output: 2 1 2 60 Description: In first case "ab" & "ba" are two different words. In third case, note that A & a are different alphabets and hence "Aa" & "aA" are different words.

# cook your dish here MOD = 1000000007 fact_mods = [0] * (501) fact_mods[0], fact_mods[1] = 1, 1 for i in range(2, 501): fact_mods[i] = (fact_mods[i-1]*i) % MOD for _ in range(int(input())): s = input() n = len(s) counts = {} denom = 1 for ch in s: counts[ch] = counts.get(ch,0) + 1 for ch in counts: denom = (denom * fact_mods[counts[ch]]) % MOD print(fact_mods[n]*pow(denom,MOD-2,MOD) % MOD)

train

APPS_structured

*Shamelessly stolen from Here :)* Your server has sixteen memory banks; each memory bank can hold any number of blocks. You must write a routine to balance the blocks between the memory banks. The reallocation routine operates in cycles. In each cycle, it finds the memory bank with the most blocks (ties won by the lowest-numbered memory bank) and redistributes those blocks among the banks. To do this, it removes all of the blocks from the selected bank, then moves to the next (by index) memory bank and inserts one of the blocks. It continues doing this until it runs out of blocks; if it reaches the last memory bank, it wraps around to the first one. We need to know how many redistributions can be done before a blocks-in-banks configuration is produced that has been seen before. For example, imagine a scenario with only four memory banks: * The banks start with 0, 2, 7, and 0 blocks (`[0,2,7,0]`). The third bank has the most blocks (7), so it is chosen for redistribution. * Starting with the next bank (the fourth bank) and then continuing one block at a time, the 7 blocks are spread out over the memory banks. The fourth, first, and second banks get two blocks each, and the third bank gets one back. The final result looks like this: 2 4 1 2. * Next, the second bank is chosen because it contains the most blocks (four). Because there are four memory banks, each gets one block. The result is: 3 1 2 3. * Now, there is a tie between the first and fourth memory banks, both of which have three blocks. The first bank wins the tie, and its three blocks are distributed evenly over the other three banks, leaving it with none: 0 2 3 4. * The fourth bank is chosen, and its four blocks are distributed such that each of the four banks receives one: 1 3 4 1. * The third bank is chosen, and the same thing happens: 2 4 1 2. At this point, we've reached a state we've seen before: 2 4 1 2 was already seen. The infinite loop is detected after the fifth block redistribution cycle, and so the answer in this example is 5. Return the number of redistribution cycles completed before a configuration is produced that has been seen before. People seem to be struggling, so here's a visual walkthrough of the above example: http://oi65.tinypic.com/dmshls.jpg Note: Remember, memory access is very fast. Yours should be too. **Hint for those who are timing out:** Look at the number of cycles happening even in the sample tests. That's a _lot_ of different configurations, and a lot of different times you're going to be searching for a matching sequence. Think of ways to cut down on the time this searching process takes. Please upvote if you enjoyed! :)

from operator import itemgetter def mem_alloc(banks): cache = set() count = 0 while tuple(banks) not in cache: cache.add(tuple(banks)) count += 1 ind, val = max(enumerate(banks), key=itemgetter(1)) banks[ind] = 0 for i in range(val): ind += 1 banks[ind % len(banks)] += 1 return count

train

APPS_structured

There's an array A consisting of N non-zero integers A1..N. A subarray of A is called alternating if any two adjacent elements in it have different signs (i.e. one of them should be negative and the other should be positive). For each x from 1 to N, compute the length of the longest alternating subarray that starts at x - that is, a subarray Ax..y for the maximum possible y ≥ x. The length of such a subarray is y-x+1. -----Input----- - The first line of the input contains an integer T - the number of test cases. - The first line of each test case contains N. - The following line contains N space-separated integers A1..N. -----Output----- For each test case, output one line with N space-separated integers - the lengths of the longest alternating subarray starting at x, for each x from 1 to N. -----Constraints----- - 1 ≤ T ≤ 10 - 1 ≤ N ≤ 105 - -109 ≤ Ai ≤ 109 -----Example----- Input: 3 4 1 2 3 4 4 1 -5 1 -5 6 -5 -1 -1 2 -2 -3 Output: 1 1 1 1 4 3 2 1 1 1 3 2 1 1 -----Explanation----- Example case 1. No two elements have different signs, so any alternating subarray may only consist of a single number. Example case 2. Every subarray is alternating. Example case 3. The only alternating subarray of length 3 is A3..5.

def g(n): s=list(map(int,input().split())) count=1 l=[] i=0 iter=0 while i<n: count=1 for j in range(i+1,n): if s[j]*s[j-1]<0: count+=1 else: break while count>0: l.append(count) count-=1 i+=1 if len(l)!=n: l.append(1) return " ".join(str(i) for i in l) t=int(input()) for i in range(t): n=int(input()) print(g(n))

train

APPS_structured

[BasE91](http://base91.sourceforge.net/) is a method for encoding binary as ASCII characters. It is more efficient than Base64 and needs 91 characters to represent the encoded data. The following ASCII charakters are used: 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789' '!#$%&()*+,./:;<=>?@[]^_`{|}~"' Create two functions that encode strings to basE91 string and decodes the other way round. b91encode('test') = 'fPNKd' b91decode('fPNKd') = 'test' b91decode('>OwJh>Io0Tv!8PE') = 'Hello World!' b91encode('Hello World!') = '>OwJh>Io0Tv!8PE' Input strings are valid.

# yet another rewrite of Joachim Henke's C# implementation ENCODE = list("ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789!#$%&()*+,./:;<=>?@[]^_`{|}~\"") DECODE = dict(map(reversed, enumerate(ENCODE))) def b91encode(s): b, i = 0, 0 r = "" for c in s: b |= ord(c) << i i += 8 if i > 13: v = b & 0x1FFF k = 13 if v < 89: v = b & 0x3FFF k += 1 b >>= k i -= k r += ENCODE[v % 91] + ENCODE[v // 91] if i: r += ENCODE[b % 91] if i > 7 or b > 90: r += ENCODE[b // 91] return r def b91decode(s): v, b, i = -1, 0, 0 r = "" for c in s: c = DECODE[c] if ~v: v += c * 91 b |= v << i i += 13 + (v & 0x1FFF < 89) while 1: r += chr(b & 0xFF) b >>= 8 i -= 8 if i < 8: break v = -1 else: v = c if ~v: r += chr((b | v << i) & 0xFF) return r

train

APPS_structured

There are some candies that need to be distributed to some children as fairly as possible (i.e. the variance of result needs to be as small as possible), but I don't know how to distribute them, so I need your help. Your assignment is to write a function with signature `distribute(m, n)` in which `m` represents how many candies there are, while `n` represents how many children there are. The function should return a container which includes the number of candies each child gains. # Notice 1. *The candy can't be divided into pieces.* 2. The list's order doesn't matter. # Requirements 1. The case `m < 0` is equivalent to `m == 0`. 2. If `n <= 0` the function should return an empty container. 3. If there isn't enough candy to distribute, you should fill the corresponding number with `0`. # Examples ```python distribute(-5, 0) # should be [] distribute( 0, 0) # should be [] distribute( 5, 0) # should be [] distribute(10, 0) # should be [] distribute(15, 0) # should be [] distribute(-5, -5) # should be [] distribute( 0, -5) # should be [] distribute( 5, -5) # should be [] distribute(10, -5) # should be [] distribute(15, -5) # should be [] distribute(-5, 10) # should be [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] distribute( 0, 10) # should be [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] distribute( 5, 10) # should be [1, 1, 1, 1, 1, 0, 0, 0, 0, 0] distribute(10, 10) # should be [1, 1, 1, 1, 1, 1, 1, 1, 1, 1] distribute(15, 10) # should be [2, 2, 2, 2, 2, 1, 1, 1, 1, 1] ``` # Input 1. m: Integer (m <= 100000) 2. n: Integer (n <= 1000) # Output 1. [Integer]

def distribute(m, n): if m <= 0: return [0]*n elif n <= 0: return [] else: a,b = divmod(m, n) return [a]*n if b == 0 else [a+1]*b + [a]*(n-b)

train

APPS_structured