长程 Transformer 模型

本文由 Teven Le Scao、Patrick Von Platen、Suraj Patil、Yacine Jernite 和 Victor Sanh 共同撰写。

每个月，我们都会选择一个重点主题，阅读有关该主题的最近发表的四篇论文。然后，我们会写一篇简短的博文，总结这些论文各自的发现及它们呈现出的共同趋势，并阐述它们对于我们后续工作的指导意义。2021 年 1 月的主题是 稀疏性和剪枝，本月 (2021 年 2 月)，我们的主题是 transfomer 模型中的长程注意力。

引言

2018 年和 2019 年，大型 transformer 模型兴起之后，两种技术趋势迅速崛起，意在降低这类模型的计算需求。首先，条件计算、量化、蒸馏和剪枝解锁了计算受限环境中的大模型推理; 我们已经在 上一篇阅读小组帖子 中探讨了这一话题。随后，研究人员开始研究如何降低预训练成本。

特别地，大家的工作一直围绕一个核心问题: transformer 模型的内存和时间复杂度与序列长度呈二次方关系。为了高效地训练大模型，2020 年发表了大量论文来解决这一瓶颈，这些论文成果斐然，年初我们训练 transformer 模型的默认训练序列长度还是 512 或 1024，一年之内的现在，我们已经突破这个值了。

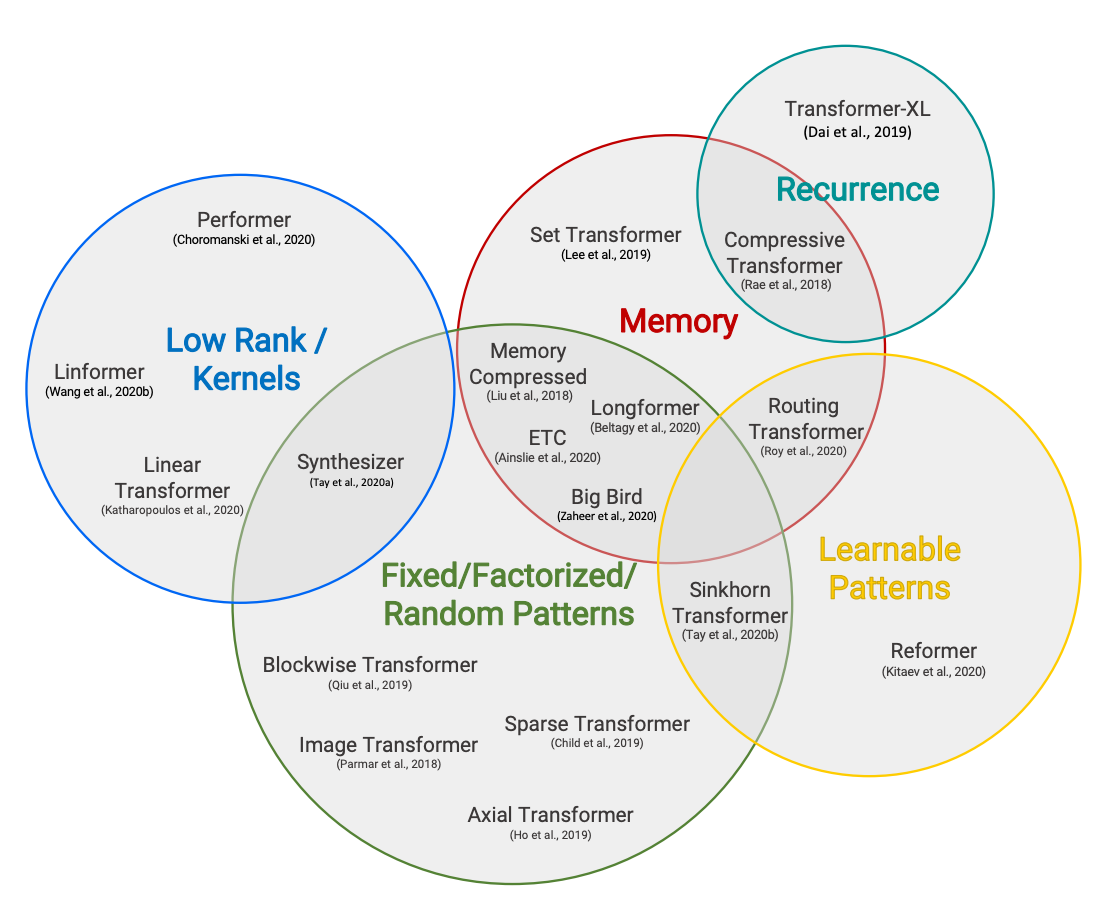
长程注意力从一开始就是我们研究和讨论的关键话题之一，我们 Hugging Face 的 Patrick Von Platen 同学甚至还专门为 Reformer 撰写了一篇 由 4 部分组成的博文。本文，我们不会试图涵盖每种方法 (太多了，根本搞不完！)，而是重点关注四个主要思想:

• 自定义注意力模式 (使用 Longformer)
• 循环 (使用 Compressive Transformer)
• 低秩逼近 (使用 Linformer)
• 核逼近 (使用 Performer)

有关这一领域的详尽概述，可阅读 Efficient Transformers: A Survey 和 Long Range Arena 这两篇综述论文。

总结

Longformer - The Long-Document Transformer

作者: Iz Beltagy, Matthew E. Peters, Arman Cohan

Longformer 通过将传统的自注意力替换为滑窗注意力 + 局部注意力 + 稀疏注意力 (参见 Sparse Transformers (2019)) 以及全局注意力的组合以解决 transformer 的内存瓶颈，使其随序列长度线性缩放。与之前的长程 transformer 模型相反 (如 Transformer-XL (2019)、Reformer (2020), Adaptive Attention Span (2019))，Longformer 的自注意力层可以即插即用直接替换标准的自注意力层，因此在长序列任务上，可以直接用它对预训练的标准注意力 checkpoint 进行进一步更新训练和/或微调。

标准自注意力矩阵 (图 a) 与输入长度呈二次方关系:

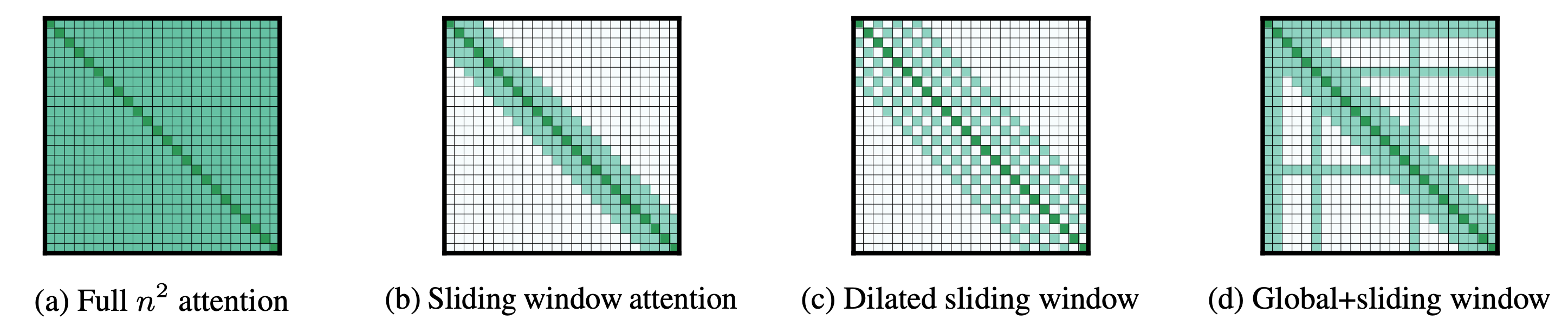
Longformer 使用不同的注意力模式执行自回归语言建模、编码器预训练和微调以及序列到序列任务。

• 对于自回归语言模型，通过将因果自注意力 (如 GPT2) 替换为膨胀滑窗自注意力 (dilated windowed self-attention) (如图 c) 以获得最佳的结果。由于 $n$ 是序列长度，$w$ 是滑窗长度，这种注意力模式将内存消耗从 $n^2$ 减少到 $wn$ ，当 $w << n$ 时，其随序列长度线性缩放。
• 对于编码器预训练，Longformer 将双向自注意力 (如 BERT) 替换为局部滑窗和全局双向自注意力的组合 (如图 d)，从而将内存消耗从 $n^2$ 减少到 $w n + g n$，这里 $g$ 是全局关注的词元数量。因此其与序列长度也呈线性关系。
• 对于序列到序列模型，只有编码器层 (如 BART) 被替换为局部和全局双向自注意力的组合 (图 d)，因为对于大多数序列到序列任务，只有编码器会处理非常长的输入 (例如摘要任务)。因此，内存消耗从 $n_s^2+ n_s n_t +n_t^2$ 减少到 $w n_s +gn_s +n_s n_t +n_t^2$ ，其中 $n_s$ 和 $n_t$ 分别是源 (编码器输入) 和目标 (解码器输入) 序列长度。为了使 Longformer 编码器 - 解码器高效运作，我们假设 $n_s$ 比 $n_t$ 大得多。

论文主要发现

• 作者提出了膨胀滑窗自注意力机制 (如图 c)，并表明与仅使用滑窗注意力或稀疏自注意力 (如图 b) 相比，其在语言建模任务上的表现更优。窗口大小随着层而增加。实验表明，这种模式在下游基准测试中优于以前的架构 (如 Transformer-XL 或自适应跨度注意力)。
• 全局注意力允许信息流经整个序列，而将全局注意力应用于任务驱动的词元 (例如问答任务中的问题词元、句子分类任务中的 CLS 词元) 可以在下游任务上带来更强的性能。使用这种全局模式，Longformer 可以成功用于文档级 NLP 任务的迁移学习。
• 标准预训练模型可以通过简单地用本文提出的长程自注意力替换标准自注意力，然后对下游任务进行微调来适配长输入。这避免了对长输入进行专门预训练所需的昂贵成本。

后续问题

• 膨胀滑窗自注意力的尺寸随层数而增加与计算机视觉中通过堆叠 CNN 而增加感受野的发现相呼应。这两个发现有何关联？两者之间哪些知识是可迁移的？
• Longformer 的编码器 - 解码器架构非常适合不需要长目标序列的任务 (例如摘要)。然而，对于需要长目标序列的长程序列到序列任务 (例如文档翻译、语音识别等)，特别是考虑到编码器 - 解码器模型的交叉注意力层，它该如何工作？
• 在实践中，滑动窗口自注意力依赖于许多索引操作来确保查询 - 键权重矩阵的对称性。这些操作在 TPU 上非常慢，这凸显了此类模式在其他硬件上的适用性问题。

Compressive Transformers for Long-Range Sequence Modelling

作者: Jack W. Rae, Anna Potapenko, Siddhant M. Jayakumar, Timothy P. Lillicrap

Transformer-XL (2019) 表明，在内存中缓存之前计算的层激活可以提高语言建模任务 (如 enwik8 ) 的性能。该模型不仅可以关注当前的 $n$ 个输入词元，还可以关注过去的 $n_m$ 个词元，其中 $n_m$ 是模型的记忆窗口长度。Transformer-XL 的内存复杂度为 $O(n^2+ n n_m)$，这表明对于非常大的 $n_m$，内存成本会显著增加。因此，当缓存的激活数量大于 $n_m$ 时，Transformer-XL 必须从内存中丢弃之前的激活。Compressive Transformer 通过添加额外的压缩记忆来有效缓存之前的激活 (否则其会被丢弃) 来解决这个问题。通过这种方式，模型可以更好地学习长程序列依赖性，从而可以访问更多的之前激活。

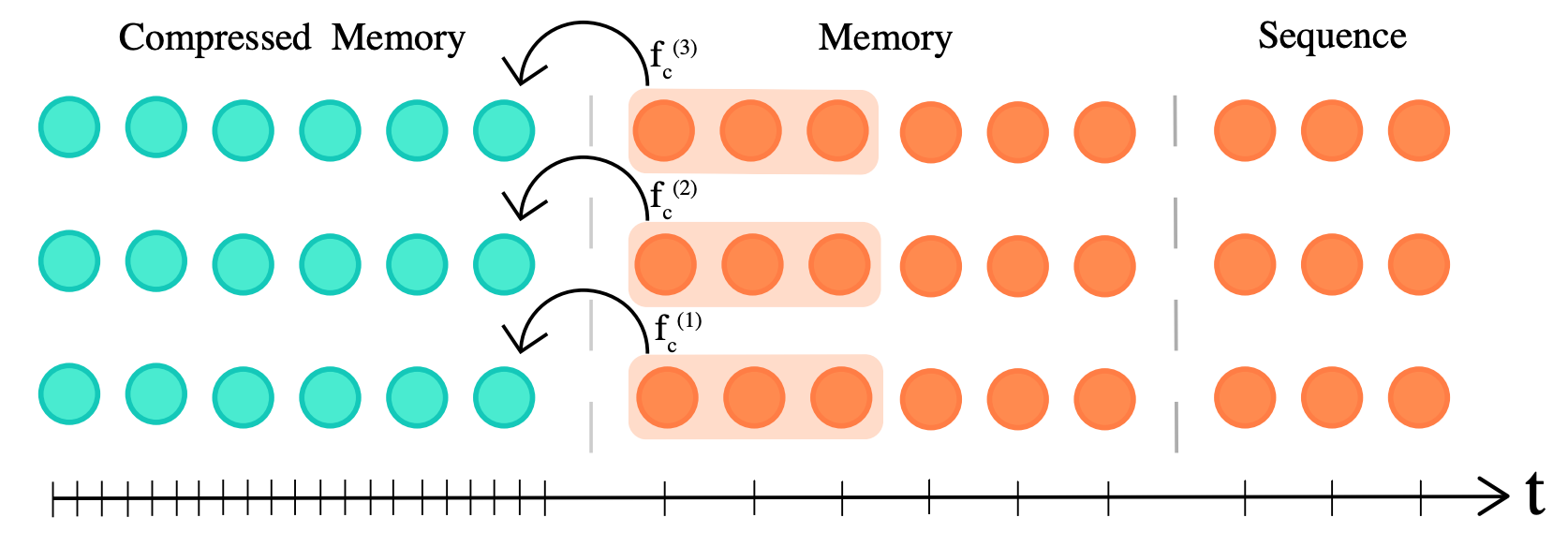
压缩因子 $c$ (图中取值为 3) 可用于决定之前激活的压缩率。作者尝试了不同的压缩函数 $f_c$，例如最大池化/均值池化 (无参数) 和一维卷积 (可训练参数)。压缩函数通过时间反向传播或局部辅助压缩损失进行训练。除了长度为 $n$ 的当前输入之外，该模型还关注常规记忆中的 $n_m$ 缓存激活以及 $n_{cm}$ 压缩记忆的激活，从而实现长度为 $l × (n_m + c n_{cm})$ 的长程依赖性，其中 $l$ 是注意力层数。这使得与 Transformer-XL 相比，其关注范围额外增加了 $l × c × n_{cm}$ 个词元，相应地，内存成本达到了 $O(n^2+ n n_m+ n n_{cm})$。作者在强化学习、音频生成和自然语言处理等一系列任务上对算法进行了实验。作者还介绍了一种新的称为语言建模基准，称为 PG19。

论文主要发现

• Compressive Transformer 在 enwik8 和 WikiText-103 数据集上得到的困惑度显著优于当前最先进的语言建模性能。特别地，压缩记忆对建模在长序列上出现的稀有词起着至关重要的作用。
• 作者表明，该模型通过越来越多地关注压缩记忆而不是常规记忆来学习如何保留显著信息，这有效牵制了旧记忆访问频率较低的趋势。
• 所有压缩函数 (平均池化、最大池化、一维卷积) 都会产生相似的结果，这证明记忆压缩是存储过去信息的有效方法。

后续问题

• Compressive Transformer 需要一个特殊的优化调度器，在训练过程中逐渐增加有效 batch size，以避免较低学习率带来的显著性能下降。这种效应尚未得到很好的理解，需要进行更多分析。
• 与 BERT 或 GPT2 等简单模型相比，Compressive Transformer 具有更多的超参数: 压缩率、压缩函数及损失、常规和压缩记忆大小等。目前尚不清楚这些参数是否可以很好地泛化到除语言建模之外的不同任务中。还是说我们会重演学习率的故事，参数的选择会使得训练非常脆弱。
• 探测常规记忆和压缩记忆来分析在长序列中我们到底记忆了什么样的信息，这是个有意思地课题。揭示最显著的信息可以为诸如 Funnel Transformer 之类的方法提供信息，这些方法减少了维护全长词元序列所带来的冗余。

Linformer: Self-Attention with Linear Complexity

作者: Sinong Wang, Belinda Z. Li, Madian Khabsa, Han Fang, Hao Ma

目标还是将自注意力相对于序列长度 $n$ 的复杂度从二次降低到线性。本文观察到注意力矩阵是低秩的 (即其 $n × n$ 矩阵的信息含量并不满)，并探讨了使用高维数据压缩技术来构建更内存高效的 transformer 的可能性。

该方法的理论基础是约翰逊 - 林登斯特劳斯引理 (Johnson-Lindenstrauss lemma)。我们考虑高维空间中的 $m$ 个点。我们希望将它们投影到低维空间，同时在误差界 $varepsilon$ 内保留数据集的结构 (即点与点之间的相互距离)。约翰逊 - 林登斯特劳斯引理指出，我们可以选择一个小维度 $k \sim 8 \log(m) / \varepsilon^2$ 并通过简单地对随机正交投影进行尝试，就可以在多项式时间内找到一个到 $R^{k}$ 的合适投影。

Linformer 通过学习注意力上下文矩阵的低秩分解，将序列长度投影到更小的维度。然后可以巧妙地重写自注意力的矩阵乘法，这样就不需要计算和存储大小为 $n × n$ 的矩阵。

标准 transformer:

$$\text{Attention}(Q, K, V) = \text{softmax}(Q * K) * V$$

              (n * h)	            (n * n)   (n * h)

Linformer:

$$\text{LinAttention}(Q, K, V) = \text{softmax}(Q * K * W^K) * W^V * V$$

              (n * h)	            (n * d)   (d * n)   (n * h)

论文主要发现

• 自注意力矩阵是低秩的，这意味着它的大部分信息可以通过其最大的几个特征值来恢复，并且可以通过低秩矩阵来近似。
• 很多工作都集中在降低隐藏状态的维数上。本文表明，通过学习投影来减少序列长度可能是一个强有力的替代方案，同时将自注意力的内存复杂度从二次降低为线性。
• 增加序列长度并不会影响 Linformer 的推理时间，而 transformer 的推理时间需要随之线性增加。此外，Linformer 自注意力并不影响收敛速度 (更新次数)。

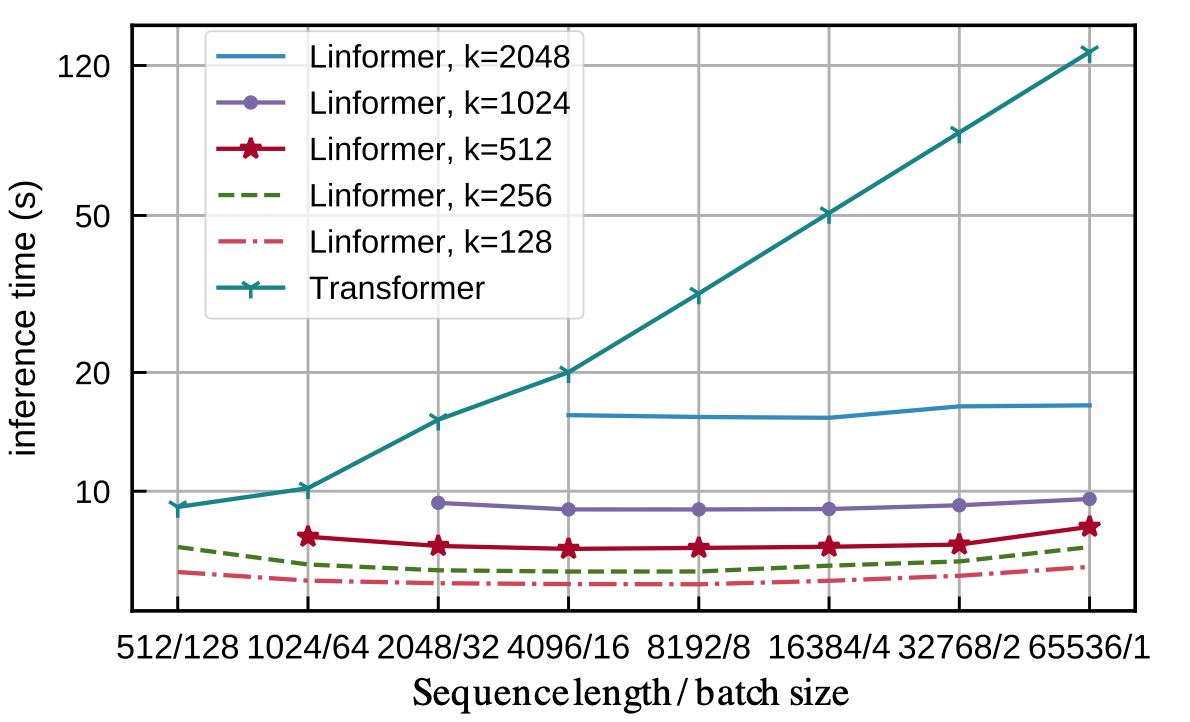
后续问题

• 尽管我们在各层之间共享投影矩阵，但此处提出的方法与约翰逊 - 林登斯特劳斯引理还是有所不同，约翰逊 - 林登斯特劳斯引理指出随机正交投影就足够了 (在多项式时间内)。随机预测在这里有用吗？这让人想起 Reformer，它在局部敏感哈希中使用随机投影来降低自注意力的内存复杂度。

Rethinking Attention with Performers

作者: Krzysztof Choromanski, Valerii Likhosherstov, David Dohan, Xingyou Song, Andreea Gane, Tamas Sarlos, Peter Hawkins, Jared Davis, Afroz Mohiuddin, Lukasz Kaiser, David Belanger, Lucy Colwell, Adrian Weller

本文的目标还是将自注意力相对于序列长度 $n$ 的复杂度从二次降低到线性。与其他论文相比，作者指出，自注意力的稀疏性和低秩先验可能并不适用于其他模态数据 (如语音、蛋白质序列建模)。因此，本文探索了在我们对自注意力矩阵没有任何先验知识的情况下，有什么可以减轻自注意力的内存负担的方法。

作者观察到，如果可以甩掉 softmax 直接执行矩阵乘法 $K × V$ ( $\text{softmax}(Q × K) × V$ )，我们就不必计算大小为 $n \times n$ 的 $Q \times K$ 矩阵，这个矩阵是内存瓶颈的来源。他们使用随机特征图 (又名随机投影) 通过以下方式近似 softmax:

$$\text{softmax}(Q * K) \sim Q’ * K’ = \phi(Q)* \phi(K)$$

, 其中 $phi$ 是一个合适的非线性函数。进而:

$$\text{Attention}(Q, K, V) \sim \phi(Q) _(\phi(K)_ V)$$

受 21 世纪初的那些机器学习论文的启发，作者引入了 FAVOR+ ( F ast A ttention V ia O rthogonal R andom positive ( + ) F eatures)，用于对自注意力矩阵进行无偏或近无偏估计，该估计具有均匀收敛和低估计方差的特点。

论文主要发现

• FAVOR+ 可用于高精度地近似自注意力矩阵，而注意力矩阵的形式没有任何先验，因此其可直接替代标准自注意力，并在多种应用及模态数据中表现出强大的性能。
• 关于在逼近 softmax 是应该怎么做，不应该怎么做的彻底的数学研究凸显了 21 世纪初开发的那些原则性方法重要性，这些工作甚至在深度学习时代都是有用的。
• FAVOR+ 还可用于对 softmax 之外的其他可核化注意力机制进行有效建模。

后续问题

• 虽然这种注意力机制近似逼近方法的误差界很紧，但即便是微小的错误，还是会通过 transformer 层传播。这就有可能在用 FAVOR+ 作为自注意力近似来微调预训练网络时带来收敛性和稳定性问题。
• FAVOR+ 算法使用了多种技术。目前尚不清楚这些技术中的哪一个对实际性能具有影响最大，尤其是在多模态场景下，有可能各个模态的状况还会不一样。

读书小组的讨论

用于自然语言理解和生成的基于 transformer 的预训练语言模型的发展突飞猛进。如何让这些系统能够高效地用于生产已成为一个非常活跃的研究领域。这强调了我们在方法和实践方面仍然有很多东西需要学习和构建，以实现高效和通用的基于深度学习的系统，特别是对于需要对长输入进行建模的应用。

上述四篇论文提供了不同的方法来处理自注意力机制的二次方内存复杂度，并将其降低为线性复杂度。Linformer 和 Longformer 都依赖于自注意力矩阵所含的信息量并不需要 $n × n$ 这么多数据来存储这一观察 (注意力矩阵是低秩且稀疏的)。Performer 给出了一种逼近 softmax-attention 的核方法 (该方法还可以逼近除 softmax 之外的任何可核化的注意力机制)。 Compressive Transformer 提供了一种正交方法来对长程依赖关系进行递归式建模。

除了对训练的影响外，这些方法所引入的不同的归纳偏差在计算速度和模型泛化性能方面都会产生潜在的影响。特别是，Linformer 和 Longformer 会导致不同的折衷: Longformer 显式地设计了一个稀疏的自注意力模式 (固定模式)，而 Linformer 则学习自注意力矩阵的低秩矩阵分解。在我们的实验中，Longformer 的效率低于 Linformer，且当前其高度依赖于实现细节。另一方面，Linformer 的分解仅适用于固定长度的上下文长度 (在训练时固定)，其在没有特定适配的情况下无法推广到更长的序列。此外，它无法缓存以前的激活，这在内容生成场景中非常有用。有趣的是，Performer 在概念上有所不同: 它学习 softmax 注意力的近似核函数，而不依赖于任何稀疏性或低秩假设。对于不同数量的训练数据，如何比较这些归纳偏差，也是个需要讨论的问题。

所有这些工作都强调了自然语言中对长输入进行建模的重要性。在行业中，经常会遇到文档翻译、文档分类或文档摘要等用例，这些用例需要以高效且稳健的方式对很长的序列进行建模。最近，零样本潜觉 (如 GPT3) 也成为标准微调的一种有前途的替代方案，其可通过增加潜觉示例的数量 (即上下文大小) 稳步提高性能和鲁棒性。最后，在语音或蛋白质等其他模态数据的建模中，也经常会遇到长度超出 512 的长序列。

对长输入进行建模与对短输入进行建模并不割裂，而应该从连续的角度来思考从较短序列到较长序列的过渡。 Shortformer、Longformer 和 BERT 提供的证据表明，在短序列上训练模型并逐渐增加序列长度可以加快训练速度并增强模型的下游性能。这一观察结果与直觉相一致，即当可用数据很少时，训得的长程依赖关系可能来自于幻觉式相关，而非来自真正的强大的语言理解。这与 Teven Le Scao 在语言建模方面进行的一些实验相呼应: 与 transformer 相比，LSTM 在小数据环境中学习效果更好，其在小规模语言建模基准 (例如 Penn Treebank) 上表现出更好的困惑度。

从实践的角度来看，位置嵌入问题也是计算效率折衷的一个重要的方面。相对位置嵌入 (在 Transformer-XL 中引入 , Compressive Transformers 也使用了它) 很有吸引力，因为它们可以轻松扩展到尚未见过的序列长度，但与此同时，相对位置嵌入的计算成本很高。另一方面，绝对位置嵌入 (在 Longformer 和 Linformer 中使用) 在处理比训练期间看到的序列更长的序列不太灵活，但计算效率更高。有趣的是，Shortformer 引入了一种简单的替代方案，将位置信息添加到自注意力机制的查询和键中，而不是将其添加到词元嵌入中。该方法称为位置注入注意力，其被证明非常高效，且产生了很好的结果。

@Hugging Face 🤗: 长程建模

用户可在 transformers 库和 模型 Hub 中找到 Longformer 的实现及其相应的开源 checkpoint。 Performer 和 Big Bird 是一种基于稀疏注意力的长程模型，目前也已支持。如果你想知道如何为 transformers 做贡献但不知道从哪里开始，可以通过论坛或 GitHub 告诉我们！

如需进一步阅读，我们建议阅读 Patrick Platen 的 Reformer 论文、Teven Le Scao 关于 约翰逊 - 林登斯特劳斯逼近的帖子 以及 Efficient Transfomers: A Survey、Long Range Arena: A Benchmark for Efficient Transformers 这两篇论文。